Question

A cube of side \[2\,m\] is placed in front of a concave mirror of focal length \[1\,m\] with its face P at a distance of \[3\,m\] and face B at a distance of \[5\,m\] form the mirror. The distance between the images of faces A and B and heights of images of A and B are,respectively

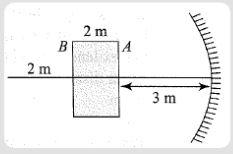
A. \[1{\text{ }}m,\,0.5{\text{ }}m,\,0.25{\text{ }}m\]
B. \[0.5{\text{ }}m,\,1\,m,\,0.25{\text{ }}m\]
C. \[0.5\,m,\,0.25\,m,\,1\,m\]
D. \[0.25\,m,\,1\,m,\,0.5\,m\]

Answer 1

Hint: First using the mirror equation to find the distance between the two points \[{v_A}\] and \[{v_B}\] then use the magnification relation to find the height of the images for point A and point B.
The formula for the mirror equation is
\[\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{v}{f}\]
Here we have to also use the magnification relation. Lens magnification is known as the ratio of an image’s height to an object’s height.
The formula for magnification is \[\dfrac{{{\text{Image}}\,{\text{height}}}}{{{\text{Object}}\,{\text{height}}}}{\text{ = -}}\dfrac{{{\text{Image}}\,{\text{distance}}}}{{{\text{Object}}\,{\text{distance}}}}\]

Complete step by step answer:
Here,
By using the mirror equation,
\[\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{v}{f}\]
Here,
For point A,
\[\dfrac{1}{{{v_A}}} = - 1 + \dfrac{1}{3} = - \dfrac{2}{3}\]
So,
\[{v_A} = - \dfrac{3}{2} = - 1.5\]
Again,
For point B,
\[\dfrac{1}{{{v_B}}} = - 1 + \dfrac{1}{5} = - \dfrac{4}{5}\]
So,
\[{v_B} = - \dfrac{5}{4} = - 1.25\]
Therefore,
The distance between two points is \[ = 1.5 - 1.25 = 0.25\,m\]
Now,
Using the magnification relation, we know that,
\[\dfrac{{{\text{Image}}\,{\text{height}}}}
{{{\text{Object}}\,{\text{height}}}}{\text{ = - }}\dfrac{{{\text{Image}}\,{\text{distance}}}}
{{{\text{Object}}\,{\text{distance}}}}\] …… (1)
Therefore,
For point A,
Image height \[ = - 2 \times \dfrac{{ - 1.5}}{{ - 3}} = - 1\,m{\text{ = 1}}\,m\] …… (Using equation (1))
And,
For point B,
Image height \[ = - 2 \times \dfrac{{ - 1.25}}{{ - 5}} = - 0.5\,m{\text{ = 0}}{\text{.5}}\,m\]
               …… (Using equation (1))
Hence,
The distance between two points is \[{\text{0}}{\text{.25}}\,m\]
Image height for point A is \[{\text{1}}\,m\]
Image height for point B is \[{\text{0}}{\text{.5}}\,m\]

Note: An optical system's focal length is a measure of how intensely the system converges or diverges light; it's the opposite of the optical strength of the system. A positive focal length means that light is converged by a system, while a negative focal length implies light is diverged by the system.A curved mirror is a mirror with a curved surface which reflects. The surface can be convex or concave. Many curved mirrors have surfaces shaped like part of a sphere but often other shapes are used in optical devices. Magnification is the method of enlarging something's apparent size, not its physical size.