Question

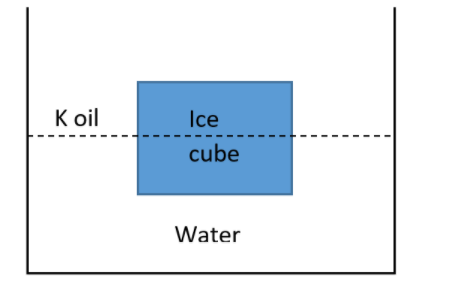
A cube of ice floats partially in water and partially in K.oil. Calculate the ratio of the volume of ice immersed in water to that in K.oil. The specific gravity of ice is \[0.9\] and that of K.oil is \[0.8\].

Answer 1

Hint: The density of the ice cube will be the product of the density of water at $4{}^\circ C$and the specific gravity. Using this find the total mass of the cube. The find the total weight of the ice cube. By the law of the Flotation, the total buoyant force by the water and the Kerosene oil will be equivalent to the weight of the ice cube. Substitute the values in it. This will help you in answering this question.

Complete step by step answer:
Let us assume that the volume of ice in water be $a{{m}^{3}}$ and the volume of ice in K.oil be $b{{m}^{3}}$. Hence the total volume can be written as,
$V=a+b$
The density of the ice cube will be the product of the density of water at $4{}^\circ C$and the specific gravity. That is we can write that,
${{d}_{ice}}={{d}_{w}}\times \rho $
Where $\rho $ be the specific gravity of the ice. This is given as,
$\rho =0.9$
And the specific gravity of oil is given as,
\[{\rho }'=0.8\]
And the density of water at $4{}^\circ C$will be,
${{d}_{w}}=1000kg{{m}^{-3}}$
Substituting the values in it,
${{d}_{ice}}=0.9\times 1000=900kg{{m}^{-3}}$
Hence, the total mass of the cube will be,
$m={{d}_{ice}}\times V$
That is,
$m=\left( a+b \right)\times 900$
The total weight of the cube will be,
\[W=\left( a+b \right)\times 900\times 10\]
By the law of the Flotation, the total buoyant force by the water and the Kerosene oil will be equivalent to the weight of the ice cube.
Therefore we can write that,
\[\text{total buoyant force}=a\times 1000+b\times 800\]
Total buoyant force can be written as,
\[\text{total buoyant force}=\left( a+b \right)\times 900\]
Substituting this in the equation will give,
\[\left( a+b \right)\times 900=a\times 1000+b\times 800\]
Rearranging the equation will give,
\[\begin{align}
  & 900a+900b=1000a+800b \\
 & \Rightarrow 100a=100b \\
 & \therefore a=b \\
\end{align}\]
As the volumes are obtained as equal, then the ratio of their volume will be \[1:1\]. Thus the question has been answered.

Note:
Buoyant force is otherwise called buoyancy. It is the force which results in the floating of objects. This force acts on an object that is partially or completely immersed in a fluid. Buoyant force is because of the differences in pressure experienced on opposite sides of a body immersed in a static fluid.