Question

A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?

Answer 1

Hint: The question is framed as a problem of projectile motion. In projectile motion, the maximum horizontal distance or the maximum range is attained when the angle of projection is $\dfrac{\pi }{4}$. Then use the third law of motion to find the height attained when the same ball is thrown vertically.

Formula Used:
The equation to find the range of a projectile:
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$
The third equation of motion:
${v^2} - {u^2} = 2aH$

Complete step by step answer:
The question paints a scenario such that a cricketer throws a ball in projectile motion and we are asked to find the maximum height attained during this motion when it achieved a maximum distance of 100 m. In projectile motion, the maximum horizontal distance or the maximum range is attained when the angle of projection is $\dfrac{\pi }{4}$. Additionally, we are later asked to calculate the maximum height when the same ball is thrown vertically upwards.
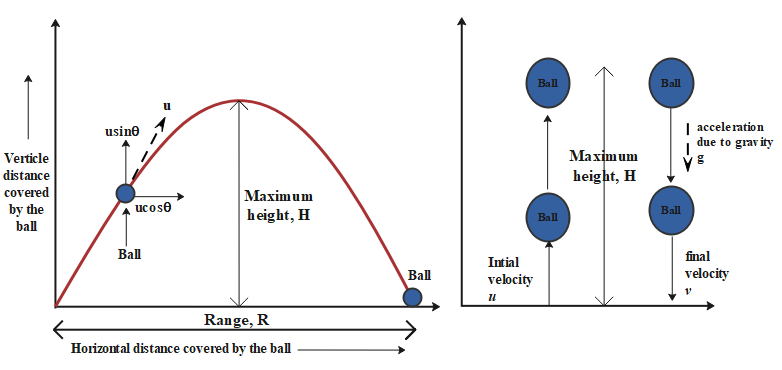
The following diagram on the left-hand side shows the projectile motion of the ball. And the diagram on the right-hand side dissipates the upwards vertical motion of the same ball.

Given:
The maximum distance or range, $R = 100m$
The angle of incidence of projectile motion, $\theta = \dfrac{\pi }{4}$

The equation to find the range of a projectile is given by:
$R = \dfrac{{{u^2}\sin 2\theta }}{g} \cdots \cdots \cdots \cdots \left( 1 \right)$
where
R represents the range,
u represents the initial velocity,
$\theta $ represents the angle of incidence,
and ‘g’ represents the acceleration due to gravity.
Substituting the given values in equation (1), we have:
Now, when the same ball is thrown vertically upwards, it will achieve its maximum height at a point where its velocity is zero. Let that height be denoted by H.
Also for vertically upward motion, the acceleration is negative i.e. $a = - g$
From the third equation of motion, we have:
${v^2} - {u^2} = 2aH \cdots \cdots \cdots \cdots \left( 3 \right)$
Where v represents the final velocity,
u represents the initial velocity.
a in our case is the acceleration due to gravity ( with negative sign due to direction )
and H represents the maximum height attained by the ball.
Substituting the known values in equation (3), we have:
$\eqalign{
  & {v^2} - {u^2} = 2aH \cr
  & \Rightarrow 0 - {u^2} = - 2gH{\text{ }}\left[ {\because a = - g{\text{ and }}v = 0} \right]{\text{ }} \cr
  & \Rightarrow H = \dfrac{{ - {u^2}}}{{ - 2g}} = \dfrac{{{u^2}}}{{2g}} \cr
  & \Rightarrow H = \dfrac{{100}}{2}{\text{ }}\left[ {\because R = \dfrac{{{u^2}}}{g} = 100} \right] \cr
  & \therefore H = 50m \cr} $
So, the maximum height attained by the same ball when thrown vertically upwards is 50 meters.

Note:
Students can get confused in understanding the question as they might assume that the question is asking to calculate the maximum height attained in the projectile motion itself. In order to avoid such mistakes read the question properly.