Question

A cricket mat of mass 50kg is rolled loosely in the form of a cylinder of radius 2m. Now again it is rolled tightly so that the radius becomes $\dfrac{3}{4}th$ of original value; then the ratio of moment of inertia of mat in the two cases is:
A. 1:3
B. 4:3
C. 3:5
D. 16:9

Answer 1

Hint: You could recall the expression for the moment of inertia of a cylinder along its central axis. Then, you could apply this expression for both the given cases. We know that the mass will be the same in both the cases and you could substitute the radius in as per the given conditions. You could then take the ratio and you may cancel out the common terms and thus even without substituting the values R and M you will find the required ratio.

Formula used:
Moment of inertia of a cylinder along the central axis,
$I=\dfrac{1}{2}M{{R}^{2}}$

Complete step-by-step answer:
In the question, we are given a cricket mat which has a mass of 50kg. Now this mat is being rolled twice. Once it is rolled loosely in the form of a cylinder with radius 2m then it is rolled tightly so that its radius becomes $\dfrac{3}{4}th$ of the original value. We are asked to find the ratio of its moment of inertia in both these cases.

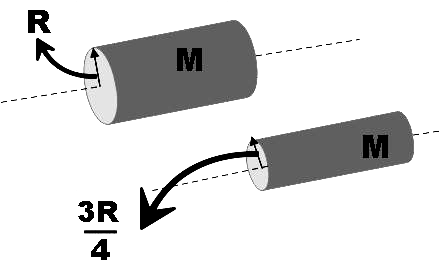
As the mat is being rolled in the form of a cylinder, let us recall the moment of inertia of a cylinder along its central axis as there is no mention of which axis specifically. So,
$I=\dfrac{1}{2}M{{R}^{2}}$
Let the radius in the first case be R, then the radius in the second case will be, $\dfrac{3}{4}R$. The mass of the mat is the same in both cases. So, the moment of inertia of the rolled mat in the first case will be,
${{I}_{1}}=\dfrac{1}{2}M{{R}^{2}}$ …………………………………… (1)
The moment of inertia in the second case will be,
${{I}_{2}}=\dfrac{1}{2}M{{\left( \dfrac{3}{4}R \right)}^{2}}$ ……………………………… (2)
Taking the ratio of (1) and (2), we get,
$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{\dfrac{1}{2}M{{R}^{2}}}{\dfrac{1}{2}M{{\left( \dfrac{3}{4}R \right)}^{2}}}$
$\Rightarrow \dfrac{{{I}_{1}}}{{{I}_{2}}}={{\left( \dfrac{4}{3} \right)}^{2}}$
$\therefore \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{16}{9}$
Therefore, we found the ratio of moment of inertia of mat in the two cases to be$16:9$. Hence, option D is the right answer.

So, the correct answer is “Option D”.

Note: Other than the central axis, a cylinder might have two other axes: one, which is along the central diameter and the other along the end diameter. Their respective moment of inertia is given by,
$I=\dfrac{1}{4}M{{R}^{2}}+\dfrac{1}{12}M{{L}^{2}}$
$I=\dfrac{1}{4}M{{R}^{2}}+\dfrac{1}{3}M{{L}^{2}}$
When there is no mention of the axis in the question, you could take it as the central axis by default.