Question

A cricket ball of mass m is hitted at the angle \[45{}^\circ \] to the horizontal with velocity v. Its kinetic energy at the topmost position is
A. 0
B. \[\dfrac{1}{2}m{{v}^{2}}\]
C. \[\dfrac{m{{v}^{2}}}{4}\]
D. \[\dfrac{m{{v}^{2}}}{2\sqrt{2}}\]

Answer 1

Hint: Since the ball is hit an angle \[45{}^\circ \] to the horizontal, velocity will be \[v\cos 45{}^\circ \]. This value of v is substituted in the formula for kinetic energy. Kinetic energy is then calculated in terms of m and v

Formula used:
Kinetic energy is given by,
     \[\text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}}\]
Where, m is mass and v is velocity.

Complete step by step answer:
A diagram can be illustrated as follows:

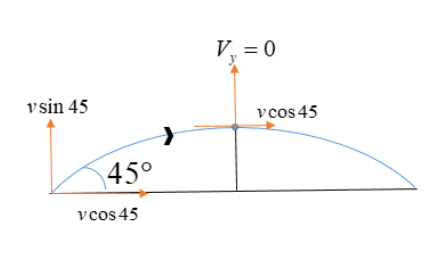
Kinetic energy is calculated as:
$\text{ K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}} $
 $ \Rightarrow \text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{\left( v\cos \theta \right)}^{2}} $
 $ \Rightarrow \text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}}{{\cos }^{2}}\theta $
 $ \Rightarrow \text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}}{{\cos }^{2}}45{}^\circ $
 $ \Rightarrow \text{K}\text{.E}\text{.}=\dfrac{1}{2}m{{v}^{2}}{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}} $
 $ \therefore \text{K}\text{.E}\text{.}=\dfrac{m{{v}^{2}}}{4} $

Therefore, kinetic energy at the topmost point is \[\dfrac{m{{v}^{2}}}{4}\].
Hence option C is the correct answer.

Additional information:
Energy transformations occur in a projectile motion, when an object moves in a curved path. When the ball is hit, the ball is moving fast, so its kinetic energy is large. As the ball rises, its speed decreases. However, according to the law of conservation of energy, the energy has to remain constant. To overcome this decrease in kinetic energy, the potential energy increases. At the topmost position, potential energy is greater and kinetic energy is smaller. When the ball starts to fall, the potential energy decreases as the kinetic energy increases.
Due to this reason, the calculated kinetic energy is less than the initial kinetic energy. The initial kinetic energy will be \[\dfrac{m{{v}^{2}}}{2}\] and the kinetic energy at the topmost position is \[\dfrac{m{{v}^{2}}}{4}\].

Note:
The vertical velocity at the topmost point is 0. If we would have taken this value instead of the horizontal velocity, we would have obtained wrong results. Also, since the problem depicts a projectile motion, it is important that we take a horizontal velocity.