Question

A crate of weight \[{F_g}\] is pushed by a force \[\overrightarrow P \] on a horizontal floor. The coefficient of static friction is \[{\mu _s}\] and \[\overrightarrow P \] is directed at angle \[\theta \] below the horizontal. The minimum value of \[P\] that will move the crate is
A. \[P = \dfrac{{{\mu _s}{F_s}\cos \theta }}{{1 - {\mu _s}\sin \theta }}\]
B. \[P = \dfrac{{{\mu _s}{F_s}\sin \theta }}{{1 - {\mu _s}\cos \theta }}\]
C. \[P = \dfrac{{{\mu _s}{F_s}\sec \theta }}{{1 - {\mu _s}\tan \theta }}\]
D. \[P = \dfrac{{{\mu _s}{F_s}{\text{cosec}}\theta }}{{1 - {\mu _s}\cot \theta }}\]

Answer 1

Hint:We are asked to find the minimum value of the applied force \[P\] so that the crate will move. First, draw a free body diagram with the given information. Form equations by balancing the forces and from these equations try to find the value of force \[P\] and check the minimum value of \[P\].

Complete step by step answer:
Given, weight of the crate \[{F_g}\].Force applied on the crate, \[\overrightarrow P \]. Coefficient of static friction, \[{\mu _s}\]. The force is applied at angle \[\theta \] below the horizontal.Let us draw a free body diagram for the given problem.

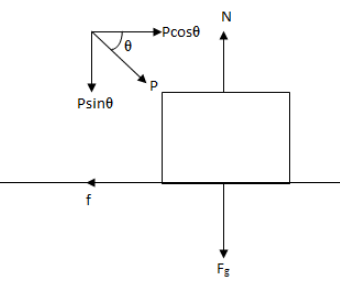
In the figure, N is the normal reaction and \[f\] is the frictional force.
From the figure above by balancing the forces vertically we get,
\[N = {F_g} + P\sin \theta \] (i)
Balancing the forces horizontally we get,
\[f = P\cos \theta \] (ii)
The static frictional force is given by the formula,
\[{f_s} = {\mu _s}N\]
where \[{\mu _s}\] is the coefficient of static friction and \[N\] is the normal reaction.
When the crate moves the frictional force will be kinetic friction and kinetic friction is less than static friction so, we can write
\[f \leqslant {\mu _s}N\] (iii)
Equating equations (ii) and (iii) we get,
\[P\cos \theta \leqslant {\mu _s}N\]
Putting the value of N from equation (i) in the above equation we get,
\[P\cos \theta \leqslant {\mu _s}\left( {{F_g} + P\sin \theta } \right)\]
\[ \Rightarrow P\cos \theta \leqslant {\mu _s}{F_g} + {\mu _s}P\sin \theta \]
\[ \Rightarrow P\cos \theta - {\mu _s}P\sin \theta \leqslant {\mu _s}{F_g}\]
\[ \Rightarrow P\left( {\cos \theta - {\mu _s}\sin \theta } \right) \leqslant {\mu _s}{F_g}\]
\[ \Rightarrow P \leqslant \dfrac{{{\mu _s}{F_g}}}{{\cos \theta - {\mu _s}\sin \theta }}\]
\[ \Rightarrow P \leqslant \dfrac{{\dfrac{{{\mu _s}{F_g}}}{{\cos \theta }}}}{{\dfrac{{\cos \theta }}{{\cos \theta }} - \dfrac{{{\mu _s}\sin \theta }}{{\cos \theta }}}}\]
\[ \Rightarrow P \leqslant \dfrac{{{\mu _s}{F_g}\sec \theta }}{{1 - {\mu _s}\tan \theta }}\]
\[ \therefore {P_{{\text{minimum}}}} = \dfrac{{{\mu _s}{F_g}\sec \theta }}{{1 - {\mu _s}\tan \theta }}\]
Therefore, the minimum value of \[P\] that will move the crate is \[\dfrac{{{\mu _s}{F_g}\sec \theta }}{{1 - {\mu _s}\tan \theta }}\].

Hence, the correct answer is option C.

Note: In such types of questions before proceeding for calculations draw a free body diagram using the given information. A free body diagram is a diagram which shows the forces acting on a system with its magnitude and direction. Also, remember kinetic friction is always less than static friction as kinetic friction is less than the applied force and static friction is greater than the applied force.