Question

A cow is tied with a rope of length 14m at the corner of a rectangular field of dimensions \[20m\times 16m\] The area of the field in which the cow can graze is:
\[\begin{align}
  & A.77{{m}^{2}} \\
 & B.140{{m}^{2}} \\
 & C.90{{m}^{2}} \\
 & D.154{{m}^{2}} \\
\end{align}\]

Answer 1

Hint: First of all, we will draw the diagram according to the given condition, then, we will observe that, we have to find the area of a quadrant of a circle having radius equal to the length of rope of which the cow is tied at the corner of a rectangular. We will use the formula of area of the quadrant of a circle as below.

Complete step-by-step answer:
\[\text{Area of quadrant = }\dfrac{\pi {{r}^{2}}}{4}\]

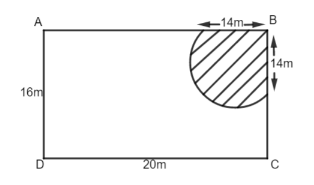
We have been given that, a cow is tied with a rope of length 14m at the corner of a rectangular field of dimensions \[20m\times 16m\] So, we have to find the area of the field in which the cow can graze.

Let us suppose the rectangular field to be ABCD and the cow is tied at corner B. Then, we can observe that the cow can graze in the quadrant of circular region having radius equals to 14m.
So, the area of the field in which the cow can graze is equal to the area of the quadrant.
We know that, \[\text{Area of quadrant = }\dfrac{\pi {{r}^{2}}}{4}\]
Where, r is the radius of the quadrant.
We have r = 14m
\[\text{Area of quadrant = }\dfrac{\pi {{\left( 14 \right)}^{2}}}{4}\]
Substituting the value of \[\pi =\dfrac{22}{7}\] we get,
\[\begin{align}
  & \text{Area of quadrant = }\dfrac{22}{7}\times \dfrac{14\times 14}{4} \\
 & \Rightarrow 154c{{m}^{2}} \\
\end{align}\]
Hence, the required area is equal to $ 154c{{m}^{2}} $
Therefore, the correct option is D.

Note: In this question, first of all the diagram is very important as we can easily observe the area that we have to find according to the condition in the question. Without drawing the diagram we think the required area will be equal to the area of the square having side 14m but this is incorrect.