Question

A corporation building is in the form as shown alongside. The vertical cross-section parallel to the width side of the building is a rectangle of size $ 5\;m \times 2\;m $ mounted by a semicircle of radius $ 1.5\;m. $ The inner measurements of a cuboid are $ 6 \times 5 \times 2\;m. $ find the volume of the corporation and the total internal surface area excluding the floor.

Answer 1

Hint: Here, we will use the standard formula to find the volume and area. Remember the difference between the total surface area and area. Place values in the equation and simplify the equations carefully. Draw, figure and frame the equation of the surface area excluding the floor accordingly.

Complete step-by-step answer:

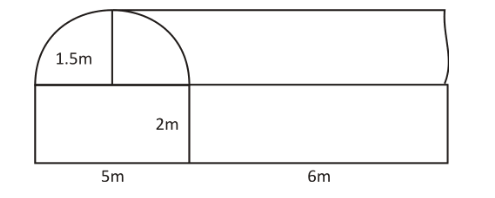
Given that –
Length of the rectangle is \[l = 5\;m\]
Breadth of the rectangle is $ b = 2\;m $
Length of the cuboid, $ L = 6\;m $
Radius of the semicircle, $ r = 1.5\;m $
Since, the corporation building is in the uniform cross-section-
Its volume is equal to the area of cross-section and length.
 $ \Rightarrow V = A \times L $
Where, Area is the sum of the area of the rectangle and the semi-circle.
 $ \Rightarrow V = [(l \times b) + (\dfrac{1}{2}\pi {r^2})] \times L $
Place values in the above equation –
 $ \Rightarrow V = [(5 \times 2) + (\dfrac{1}{2}\pi {(1.5)^2})] \times 6 $
Simplify the above equation –
 $
   \Rightarrow V = [(10) + (\dfrac{1}{2} \times \dfrac{{22}}{7} \times (2.25)] \times 6 \\
   \Rightarrow V = [10 + 3.5357] \times 6 \;
  $
Do multiplication –
 $
   \Rightarrow V = 13.5357 \times 6{\text{ }} \\
  {\text{ [}} \Rightarrow {\text{Area of cross section = 13}}{\text{.53}}{{\text{m}}^2}]{\text{ }}....{\text{(A)}} \\
   \Rightarrow V = 81.21\;{m^3} \;
  $
Now, Perimeter of cross-section excluding the floor $ = 2 + \dfrac{{2\pi r}}{2} + 2 $
Like terms cancel each other from the numerator and the denominator. Also, place values in the above equation –
Perimeter $ = 2 + \dfrac{{22}}{7} \times 1.5 + 2 $
Simplify the above equation –
Perimeter $ = 4 + 4.71 $
Perimeter $ = 8.71\;{m^{}} $ ..... (B)
Now, the total surface area excluding the floor is the sum of perimeter of the cross-section into length and two into area of cross-section (twice as we have two surfaces)
Required total surface area $ = $ Perimeter of the cross-section $ \times $ length $ + 2 \times $ area of cross-section
Place values in the above equation – by using equations (A) and (B)
Total surface area $ = 8.71 \times 6 + 2 \times 13.53 $
Simplify the above equation-
Total surface area $ = 79.32{m^2} $
Hence, the required answer – the volume and the total surface area are $ 81.21\;{m^3} $ and $ 79.32{m^2} $ respectively.
So, the correct answer is “the volume and the total surface area are $ 81.21\;{m^3} $ and $ 79.32{m^2} $ respectively.
”.

Note: Always put the correct units after the values are calculated. Remember that perimeter is measured in meters or centimetres, area in square units and the volume is measured in cube of the units. Remember all the formulas for the volume and area of the closed and open figures.