Question

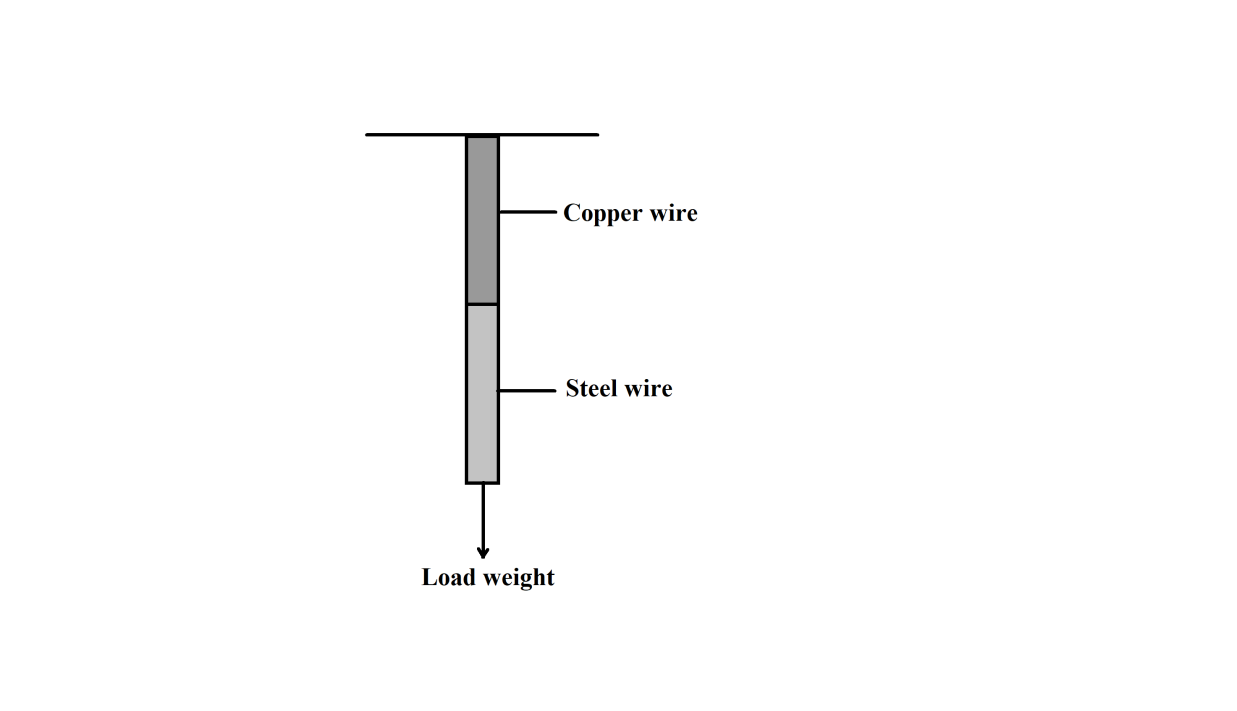
A copper wire and a steel wire of the same length and same cross section are joined end to end to form a composite wire. The composite wire is hung from a rigid support and a load is suspended from the other end. If the increase in length of the composite wire is $2.4mm$then the increase in lengths of steel and copper wires are:
$\left( {{Y}_{Cu}}=10\times {{10}^{10}}N{{m}^{-2}},{{Y}_{Steel}}=2\times {{10}^{11}}N{{m}^{-2}} \right)$
$\begin{align}
  & \text{A}\text{. }1.2mm,1.2mm\text{ } \\
 & \text{B}\text{. }0.6mm,1.8mm \\
 & \text{C}\text{. }0.8mm,1.6mm \\
 & \text{D}\text{. }0.4mm,2.0mm \\
\end{align}$

Answer 1

Hint: For determining the relation between the extensions in the two wires, we will use the concept of Young’s Modulus. As the length and area of cross-section of both the wires are the same, therefore, we will obtain a relation between the ratio of extension in the wire and their respective young’s modulus.

Formula used:
$Y=\dfrac{F}{\dfrac{AL}{\Delta l}}=\dfrac{F\Delta l}{AL}$


Complete step by step solution:
We are given that the length of Copper wire is equal to the length of Steel wire, and they both have the same area of cross section. For finding the relation in the extension in the wires, we will use the equation of Young’s Modulus. Young’s Modulus, being an internal property of an object, does not depend upon the shape and size of the body. The value of Young’s modulus is kept the same for a particular material. We have the values of Young's modulus for both the wires.

$\begin{align}
  & {{L}_{Cu}}={{L}_{Steel}} \\
 & {{A}_{Cu}}={{A}_{Steel}} \\
\end{align}$
Let’s say the increase in lengths of the individual wires be $\Delta {{l}_{Cu}}$and $\Delta {{l}_{Steel}}$
Total increase in the length of composite wire is$\Delta {{l}_{total}}$, and $\Delta {{l}_{total}}=2.4mm$
It means,
$\Delta {{l}_{Cu}}+\Delta {{l}_{Steel}}=\Delta {{l}_{total}}=2.4mm$
Also, young’s modulus of elasticity $Y=\dfrac{Fl}{A\Delta l}$
It gives, $\Delta l=\dfrac{FL}{AY}$
Now,
$\Delta {{l}_{Cu}}=\dfrac{F{{L}_{Cu}}}{{{A}_{Cu}}{{Y}_{Cu}}}=\dfrac{FL}{A{{Y}_{Cu}}}$
$\Delta {{l}_{Steel}}=\dfrac{F{{L}_{Steel}}}{{{A}_{Steel}}{{Y}_{Steel}}}=\dfrac{FL}{A{{Y}_{Steel}}}$
Dividing the above two equations,
$\dfrac{\Delta {{l}_{Cu}}}{\Delta {{l}_{Steel}}}=\dfrac{{{Y}_{Steel}}}{{{Y}_{Cu}}}$
Putting values of ${{Y}_{Steel}}$and${{Y}_{Cu}}$,
$\dfrac{\Delta {{l}_{Cu}}}{\Delta {{l}_{Steel}}}=\dfrac{2\times {{10}^{11}}}{10\times {{10}^{10}}}$
$\dfrac{\Delta {{l}_{Cu}}}{\Delta {{l}_{Steel}}}=2$
The extension in Copper wire will be double of the extension in steel wire.
As we have,
$\Delta {{l}_{Cu}}+\Delta {{l}_{Steel}}=\Delta {{l}_{total}}=2.4mm$
Put\[\Delta {{l}_{Cu}}=2\Delta {{l}_{Steel}}\]
We get,
$\begin{align}
  & \Delta {{l}_{Steel}}=0.8mm \\
 & \Delta {{l}_{Cu}}=2\Delta {{l}_{Steel}}=1.6mm \\
\end{align}$
Therefore,
$\Delta {{l}_{Steel}}$is $0.8mm$and $\Delta {{l}_{Cu}}$is $1.6mm$

Hence, the correct option is C.

Note: Students should keep in mind that Young’s modulus of a material is a fundamental property of every material that cannot be changed. For a particular material, such as Copper and Steel, young’s modulus is kept constant. If two materials have the same length and area of cross-section, the ratio of extension in the length of the wires will be inversely proportional to the ratio of young’s modulus of the two materials.