Question

A copper ball of density ${{\rho }_{C}}$​ and diameter $d$ is immersed in oil of density ${{\rho }_{0}}$​. What charge should be present on the ball, so that it could be suspended in the oil, if a homogeneous electric field $E$ is given vertically upward?
$\begin{align}
  & A.Q=\dfrac{\pi {{d}^{2}}\left( {{\rho }_{C}}-{{\rho }_{0}} \right)g}{6E} \\
 & B.Q=\dfrac{\pi {{d}^{3}}\left( {{\rho }_{C}}-{{\rho }_{0}} \right)g}{6E} \\
 & C.Q=\dfrac{\pi {{d}^{3}}\left( {{\rho }_{C}}-{{\rho }_{0}} \right)g}{E} \\
 & D.Q=\dfrac{\pi {{d}^{2}}\left( {{\rho }_{C}}-{{\rho }_{0}} \right)g}{2E} \\
\end{align}$

Answer 1

Hint: The pressure applied due to electric field is determined by taking the product of height or the depth in the oil, density difference between the copper ball and oil and also the acceleration due to gravity. Substitute the values of the terms in the given equation. The charge present in the copper ball is found by dividing the pressure applied by the oil by the electric field. These will help you to solve this question.

Formula used: $P=h\rho g$

Complete step by step answer:
First of all let us look at the terms mentioned in the question.
The copper ball is having density which is given as ${{\rho }_{C}}$. This copper ball is having a diameter $d$. The density of the oil is indicated as ${{\rho }_{0}}$. And the electric field is given as $E$.

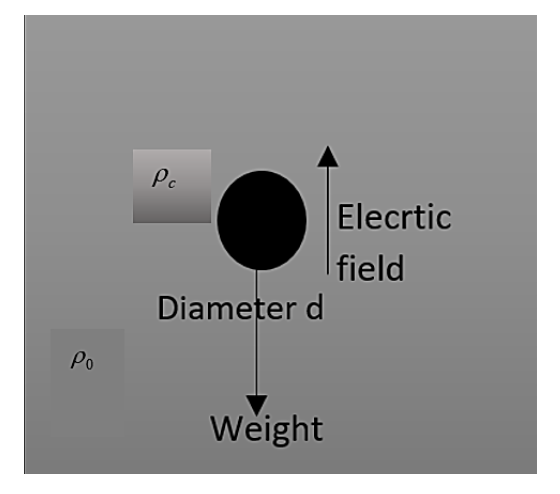
The homogeneous electric field applies a pressure on the copper ball can be found using an equation,
$P=h\rho g$
The difference in the density is given as,
$\rho ={{\rho }_{C}}-{{\rho }_{0}}$
And the value of the height is given as,
$h=\pi \dfrac{{{d}^{2}}}{6}$
Substituting this in the equation will give,
$P=\pi \dfrac{{{d}^{2}}}{6}\times \left( {{\rho }_{C}}-{{\rho }_{0}} \right)g$
And also the charge in the copper ball can be found by dividing the pressure on the ball by the electric field. Therefore we can write that,
$Q=\dfrac{P}{E}$
Substituting the values in this equation,
$Q=\dfrac{\pi \dfrac{{{d}^{2}}}{6}\times \left( {{\rho }_{C}}-{{\rho }_{0}} \right)g}{E}$

So, the correct answer is “Option A”.

Note: Fluid pressure is given as the measure of the force acting in a unit area. Fluid pressure can occur due to gravity, acceleration, or forces acting in a container. Pressure gets increased as the depth gets higher since the fluid at a lower depth should support the fluid above it also.