Question

A coolie X is carrying a load on his head climbs up a slope and another Y carrying the identical load on his head moves the same distance on the frictionless horizontal platform. Who does more work?
A. X
B. Y
C. Both A and B.
D. Cannot say

Answer 1

Hint: The amount of work done strongly depends on the angle between the force and displacement.

Complete step by step answer:
Refer to the figure below for an object moving up the inclined plane:

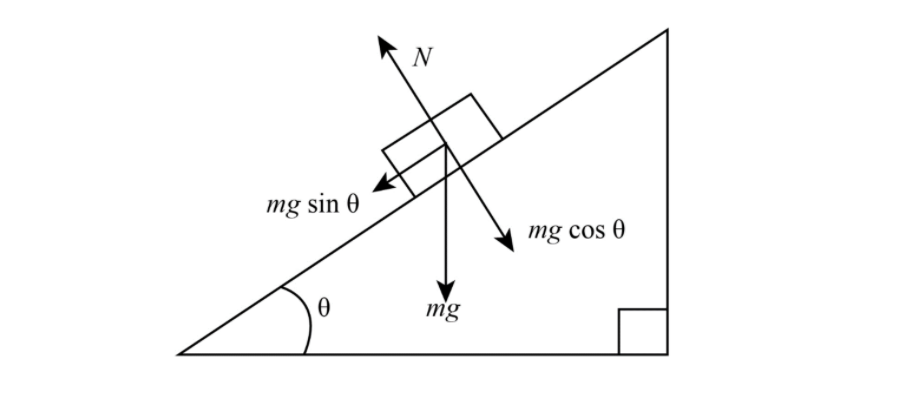
Ability to do work is called energy and the energy dissipated is equal to work done.
Express the relation for work done:
$W = F\,s\cos \theta $

Here $W$ is the work done, $F$ is the force acting on the body, $s$ is the displacement and $\theta $ is the angle between the force and the displacement.
In case of Y when it is moving on a flat surface the angle between force and displacement is $90^\circ $, and $N$ is equal to normal reaction.

Therefore, the work done in case of Y becomes,
$
  W = F\,\times s \times\cos 90^\circ \\
  W = m\,g\,\times s \times\cos 90^\circ \\
  W = 0 \\
 $
Here, $m$ is the mass of the body and $g$ is the acceleration due to gravity.
Whereas, in case of X, the force and displacement are not perpendicular. Therefore,
$W \ne 0$

Therefore, X does more work as compared to Y.

Hence the correct option is (A).

Note: Work done by X while moving up the slope is, $W = (F - mg\sin \theta ) \times s$. When X is moving up the slope, it has to encounter friction down the slope and has to work against gravity. But Y is moving on a frictionless surface.