Question

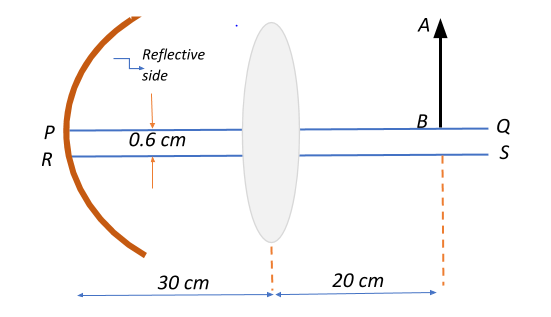
A convex lens of focal length $15\;cm$ and a concave mirror of focal length $30\;cm$ are kept with their optic axes PQ and RS parallel but separated in vertical direction by $0.6\;cm$ as shown in Fig. The distance between the lens and mirror is $30\;cm$. An upright object AB of height $1.2\;cm$ is placed on the optics axis PQ of the lens at a distance of $20\;cm$ from the lens. If $A^\prime B^\prime$ is the image after refraction from the lens and reflection from the mirror, find the distance of $A^\prime B^\prime$ from the pole of the mirror and obtain its magnification. Also, locate positions of $A^\prime$ and $B^\prime$ with respect to the optic axis RS.

Answer 1

Hint: First find the image distance for the convex lens. Then using this image as the object for the mirror calculate the image distance for the concave mirror. Simultaneously calculate the magnification produced in each case, and find the resultant magnification to deduce the final image height and location. Remember throughout that the optic axis of the lens is PQ while that of the mirror is RS as this is crucial in pointing to the location of $A^\prime B^\prime$.

Formula used:
Mirror formula: $\dfrac{1}{f} =\dfrac{1}{v}+\dfrac{1}{u}$ where f is the focal length, u is the object distance and v is the image distance.
Lens formula: $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Linear magnification of a mirror $M_{mirror} = -\;\dfrac{v}{u}$
Linear magnification of a lens $M_{lens} = \dfrac{v}{u}$

Complete step by step answer:
Let us try and understand what is given to us.
We have a convex lens and a concave mirror aligned along the horizontal axis and an object is placed near the lens.
Let us first look at the lens.
The object distance for the lens is $u_{lens} = +20\;cm$, and focal length $f_{lens} = -15\;cm$
Therefore, the image distance for the lens can be obtained as follows:
$\dfrac{1}{f_{lens}} = \dfrac{1}{v_{lens}} - \dfrac{1}{u_{lens}} \Rightarrow \dfrac{1}{v_{lens}} = \dfrac{1}{f_{lens}} + \dfrac{1}{u_{lens}} \Rightarrow \dfrac{1}{v_{lens}} = -\;\dfrac{1}{15} + \dfrac{1}{20} = \dfrac{15-20}{300} \Rightarrow \dfrac{1}{v_{lens}}= 0.01667$
$\Rightarrow v_{lens} = -\;60\;cm$. The negative sign indicates that the image is formed to the left of the lens. This means that the image formed is real.
The magnification of the lens can thus be calculated to be:
$M_{lens} = \dfrac{v_{lens}}{u_{lens}} = \dfrac{-60}{20} = -3$. The negative sign indicates that the image formed is inverted, and the image is magnified by a factor of 3.
Now, let us look at the concave mirror.
Since the object for the mirror is the image formed by the lens, the object distance for the mirror is given as $u_{mirror} = -60 +30 = -\;30\;cm$ and the focal length of the mirror is $f_{mirror} = 30\;cm$
Therefore, the image distance for the mirror can be obtained as follows:
 $\dfrac{1}{f_{mirror}} = \dfrac{1}{v_{mirror}} + \dfrac{1}{u_{mirror}} \Rightarrow \dfrac{1}{v_{mirror}} = \dfrac{1}{f_{mirror}} - \dfrac{1}{u_{mirror}} \Rightarrow \dfrac{1}{v_{mirror}} = \dfrac{1}{30} + \dfrac{1}{30} = \dfrac{2}{30} \Rightarrow v_{mirror} = 15\;cm $
This is the image $A^\prime B^\prime$ and is at a distance of $15\;cm$ from the pole of the mirror.
The magnification of the mirror can thus be calculated to be:
$M_{mirror} = -\;\dfrac{v_{mirror}}{u_{mirror}} = -\;\dfrac{15}{-30} = -0.5$. The negative sign indicates that the image formed is upright, and the image is magnified by a factor of 0.5.
Therefore, the net magnification can be calculated to be:
$M_{net} = M_{lens} \times M_{mirror} = -\;3 \times 0.5 = -\;1.5$
Therefore image $A^\prime B^\prime$ is $-\;1.5$ times the size of object AB, i.e.,
Size of $A^\prime B^\prime = -\;1.5 \times 1.2 = -\;1.8cm$. The negative sign indicates that the image is inverted.
Now we can locate $A^\prime$ and $B^\prime$ with respect to the optic axis RS. Remember that PQ is the optic axis of the lens and RS is the optic axis of the mirror.
The image of B formed by the convex lens is $0.6\;cm$ above RS (since it forms an inverted image along PQ, with the tip of B on PQ and the distance between PQ and RS is $0.6\;cm$. This image gets magnified 0.5 times by the mirror, which means that this image of B gets displaced by $0.6 \times 0.5 = 0.3\;cm$ up from RS. This means that $B^\prime$ will be $0.3\;cm$ above RS.
This means that the rest of the image lies $1.8-0.3 = 1.5\;cm$ from RS. This means that $A^\prime$ will be $1.5\;cm$ from RS.

Note:
Do not get confused with the sign and the number for magnification. The sign indicates whether the image is upright or inverted whereas the number indicates if the image is diminished in size or magnified.
$ Magnification = \dfrac{apparent(image) size}{true(object) size}$
If it is > 1 it means that the image is magnified whereas if it is between 0 and 1 the image is minified.
Therefore, total magnification is given by
$Magnification_{resultant} = \pm Magnification$
According to our above chosen convention if it is “+” it means that the image is upright whereas if it is “-“ the image is inverted.
Also, do not get confused between the sign conventions for lens and mirrors.
For a lens, the right side means negative and the left side means positive. For example, if the object is on the right side of the lens, the object distance will be negative. The same applies for image distance as well. Therefore, as you go from the left to the right side of the optic axis the sign changes from positive to negative for a lens. Also, virtual images are formed on the same side of the lens as the object whereas real images are formed on the opposite side of the lens.
However, for a concave mirror, an object placed in front of the mirror (on the reflective side) will take a negative sign, and real images are formed on the reflective side (object side) of the mirror and virtual images are formed behind the mirror.