Question

A consistent force $F = {m_1}g/2$ is applied on the block of mass ${m_2}$ as shown in figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of ${m_2}$.

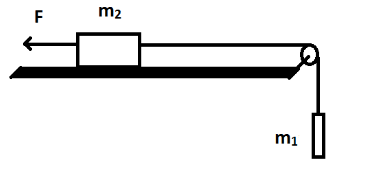
Answer 1

Hint:To solve this problem, we need to use two main concepts. First is the tensile force and second is Newton's second law of motion. We will consider the horizontal forces acting on mass ${m_2}$ and vertical forces on the mass ${m_1}$. By this we can obtain two equations which will help us find the value of the acceleration of ${m_2}$.

Complete step by step answer:
Let us consider the forces on the system as shown in figure. Let T be the tension in the rope.

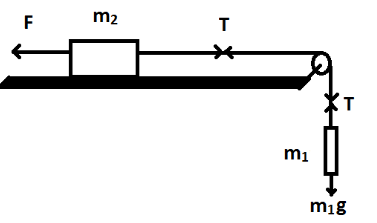
Now, we will consider the horizontal forces action on mass ${m_2}$.

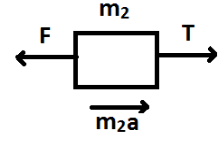
As shown in the figure, two forces are clearly visible action in the opposite direction on mass ${m_2}$. First is force F and second is the tensile force T. Moreover. If we take acceleration as a, then according to Newton’s second law of motion, there is another force ${m_2}a$acting in the right direction.
Equating these horizontal forces, we get
$F = {m_2}a + T$
It is given that $F = {m_1}g/2$
$
\dfrac{{{m_1}g}}{2} = {m_2}a + T \\
\Rightarrow T = \dfrac{{{m_1}g}}{2} - {m_2}a \\ $
Now, we will consider vertical forces acting on mass ${m_1}$.

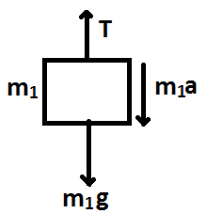
Here, tensile force is acting upwards and weight and force due to motion acts downwards.
Equating the vertical forces, we get
$T = {m_1}a + {m_1}g$
Putting $T = \dfrac{{{m_1}g}}{2} - {m_2}a$ in this equation, we get
$
\dfrac{{{m_1}g}}{2} - {m_2}a = {m_1}a + {m_1}g \\
\Rightarrow {m_1}a + {m_2}a = \dfrac{{{m_1}g}}{2} - {m_1}g \\
\Rightarrow a\left( {{m_1} + {m_2}} \right) = - \dfrac{{{m_1}g}}{2} \\
\therefore a = - \dfrac{{{m_1}g}}{{2\left( {{m_1} + {m_2}} \right)}} $

Thus the acceleration of ${m_2}$is $ - \dfrac{{{m_1}g}}{{2\left( {{m_1} + {m_2}} \right)}}$.

Note:Here, we have used Newton’s second law of motion to determine the answer of this question. This law states that the acceleration of an object is directly related to the net force and inversely related to its mass. Thus, when a force is applied on the body and if its mass is known, then the acceleration can be determined by applying this law.