
A conjecture and the two-column proof used to prove the conjecture are shown. Match each expression or phrase to the appropriate statement or reason?
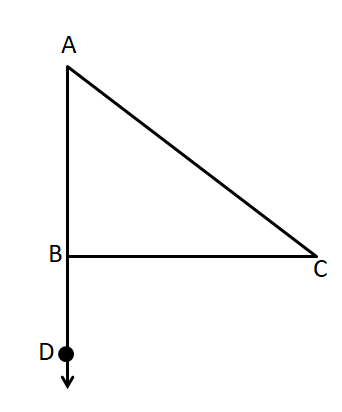
\[\angle CBD={{90}^{\circ }}\]
Prove: \[\Delta ABC\] is a right triangle
Statement Reason 1. \[\angle CBD={{90}^{\circ }}\] 1. 2. \[\angle ABC\] and \[\angle CBD\] are supplementary 2. 3. Definition of supplementary 3. \[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\] 4. 5. 5. Subtraction Property of Equality 6. \[\angle ABC\] is a right angle 6. \[\Delta ABC\] is a right triangle. 7. Definition of right triangle.

| Statement | Reason |
| 1. \[\angle CBD={{90}^{\circ }}\] | 1. |
| 2. \[\angle ABC\] and \[\angle CBD\] are supplementary | 2. |
| 3. Definition of supplementary | |
| 3. \[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\] | 4. |
| 5. | 5. Subtraction Property of Equality |
| 6. \[\angle ABC\] is a right angle | 6. |
| \[\Delta ABC\] is a right triangle. | 7. Definition of right triangle. |
Answer
527.1k+ views
Hint: In the above question, we are given the information that \[\angle CBD={{90}^{\circ }}\]using which we have to prove that \[\Delta ABC\]is a right triangle, following the sequence of the statements given in the first column of the table. In the first column of the given table, a number of statements are given to us. Also, we can see that some are missing in between. We need to fill the statements according to the proper sequence. And in the second column, the corresponding reasons are written next to the corresponding statements. The missing reasons are to be filled according to the corresponding statements.
Complete step by step solution:
Let us consider the first statement which is \[\angle CBD={{90}^{\circ }}\]. Since it has been given to us, the reason for this must be given in the question.
Now, from the second statement, we have \[\angle ABC\] and \[\angle CBD\] are supplementary. From the figure given we have
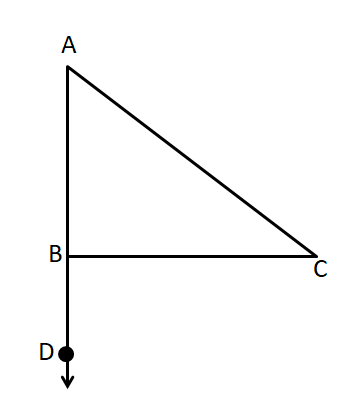
We can see in the above figure that the angles \[\angle ABC\] and \[\angle CBD\]together form a linear pair since they are the adjacent angles formed by the intersection of the lines AB and BC. Therefore, they must be supplementary. Therefore, the reason for this must be that linear pair angles are supplementary.
Now, we have a blank for the third statement. But we do have the reason for this statement, which is given as “definition of supplementary”. We know that the definition of supplementary is for the linear pair angles and states that their sum is equal to \[{{180}^{\circ }}\]. Therefore, the third statement must be
\[\Rightarrow \angle ABC+\angle CBD={{180}^{\circ }}\]
Now, the fourth statement is given as\[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\]. For this we need to substitute the first statement \[\angle CBD={{90}^{\circ }}\]into the third, \[\angle ABC+\angle CBD={{180}^{\circ }}\].
Now, the fifth statement is again blank, for which the reason is given as “Subtraction Property of Equality”. This means we need to subtract something from the above equation, which is \[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\]. Therefore, we will subtract \[{{90}^{\circ }}\]from the equation to get
\[\begin{align}
& \Rightarrow \angle ABC+{{90}^{\circ }}-{{90}^{\circ }}={{180}^{\circ }}-{{90}^{\circ }} \\
& \Rightarrow \angle ABC={{90}^{\circ }} \\
\end{align}\]
Therefore, the fifth statement must be \[\angle ABC={{90}^{\circ }}\].
Now, the sixth statement has been given as \[\angle ABC\] is a right angle. From the equation in the above statement, we have \[\angle ABC={{90}^{\circ }}\]. We know that a right angle is that whose value is equal to \[{{90}^{\circ }}\]. Therefore, the reason for this statement must be “definition of a right angle”.
The sixth statement and the sixth reason both are given to us. Therefore, the complete table will be given as
Note: For solving these types of questions, we must be familiar with the properties and concepts of line, triangles and their types etc. Also, we must be comfortable while dealing with multiple linear equations. We must not consider this question as a matching problem. All the reasons are written next to the corresponding statements.
Complete step by step solution:
Let us consider the first statement which is \[\angle CBD={{90}^{\circ }}\]. Since it has been given to us, the reason for this must be given in the question.
Now, from the second statement, we have \[\angle ABC\] and \[\angle CBD\] are supplementary. From the figure given we have

We can see in the above figure that the angles \[\angle ABC\] and \[\angle CBD\]together form a linear pair since they are the adjacent angles formed by the intersection of the lines AB and BC. Therefore, they must be supplementary. Therefore, the reason for this must be that linear pair angles are supplementary.
Now, we have a blank for the third statement. But we do have the reason for this statement, which is given as “definition of supplementary”. We know that the definition of supplementary is for the linear pair angles and states that their sum is equal to \[{{180}^{\circ }}\]. Therefore, the third statement must be
\[\Rightarrow \angle ABC+\angle CBD={{180}^{\circ }}\]
Now, the fourth statement is given as\[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\]. For this we need to substitute the first statement \[\angle CBD={{90}^{\circ }}\]into the third, \[\angle ABC+\angle CBD={{180}^{\circ }}\].
Now, the fifth statement is again blank, for which the reason is given as “Subtraction Property of Equality”. This means we need to subtract something from the above equation, which is \[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\]. Therefore, we will subtract \[{{90}^{\circ }}\]from the equation to get
\[\begin{align}
& \Rightarrow \angle ABC+{{90}^{\circ }}-{{90}^{\circ }}={{180}^{\circ }}-{{90}^{\circ }} \\
& \Rightarrow \angle ABC={{90}^{\circ }} \\
\end{align}\]
Therefore, the fifth statement must be \[\angle ABC={{90}^{\circ }}\].
Now, the sixth statement has been given as \[\angle ABC\] is a right angle. From the equation in the above statement, we have \[\angle ABC={{90}^{\circ }}\]. We know that a right angle is that whose value is equal to \[{{90}^{\circ }}\]. Therefore, the reason for this statement must be “definition of a right angle”.
The sixth statement and the sixth reason both are given to us. Therefore, the complete table will be given as
| Statement | Reason |
| 1. \[\angle CBD={{90}^{\circ }}\] | 1. Given in the question |
| 2. \[\angle ABC\] and \[\angle CBD\] are supplementary | 2. Linear pair angles are supplementary |
| 3. \[\angle ABC+\angle CBD={{180}^{\circ }}\] | 3. Definition of supplementary |
| 4. \[\angle ABC+{{90}^{\circ }}={{180}^{\circ }}\] | 4. Substitute first statement in third statement |
| 5. \[\angle ABC={{90}^{\circ }}\] | 5. Subtraction Property of Equality |
| 6. \[\angle ABC\] is a right angle | 6. Definition of right angle |
| \[\Delta ABC\] is a right triangle. | 7. Definition of right triangle.. |
Note: For solving these types of questions, we must be familiar with the properties and concepts of line, triangles and their types etc. Also, we must be comfortable while dealing with multiple linear equations. We must not consider this question as a matching problem. All the reasons are written next to the corresponding statements.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

What happens to glucose which enters nephron along class 10 biology CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




