Question

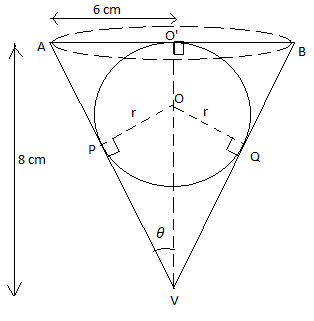
A conical vessel of radius 6cm and height 8cm is completely filled with water. A sphere is lowered into water and its size is such that when it touches the sides, it is just immersed as shown in figure. What fraction of water overflows?

Answer 1

Hint: In the above question we will use the formulae of the volume of cone and volume of sphere which are given as belows:
$\begin{align}
  & \text{volume of cone = }\dfrac{1}{3}\pi {{R}^{2}}H\text{ where R is radius and H is height}\text{.} \\
 & \text{volume of sphere = }\dfrac{4}{3}\pi {{r}^{3}}\text{ where r is the radius of the sphere}\text{.} \\
\end{align}$

Complete step-by-step answer:
We have been given R=6cm and H= 8cm.
Volume of cone\[=\dfrac{1}{3}\times \pi \times {{6}^{2}}\times 8=96\pi c{{m}^{3}}\]
 \[\begin{align}
  & \vartriangle AO'V,\text{ by pythagoras theorem:} \\
 & A{{V}^{2}}={{6}^{2}}+{{8}^{2}} \\
 & \Rightarrow AV=\sqrt{100}=10cm \\
 & \text{Hence, sin}\theta \text{=}\dfrac{O'V}{AV}=\dfrac{6}{10}=\dfrac{3}{5}...................(1) \\
 & \text{In }\vartriangle \text{POV,} \\
 & \text{ sin}\theta \text{=}\dfrac{PO}{OV}=\dfrac{r}{OV} \\
 & \text{ }\Rightarrow \text{ }\dfrac{3}{5}=\dfrac{r}{8-r} \\
 & \text{ }\Rightarrow \text{24-3r=5r} \\
 & \text{ }\Rightarrow \text{r=3cm} \\
 & \text{volume of sphere = }\dfrac{4}{3}\pi \times {{3}^{3}}\text{c}{{\text{m}}^{3}}\text{=}36\pi c{{m}^{3}}\text{ } \\
\end{align}\]
Now, volume of water = volume of cone.
Clearly, the volume of the water that flows out of the cone is the same as the volume of the sphere.
Hence, fraction of the water that flows out =\[\dfrac{\text{volume of sphere}}{\text{volume of cone}}=\dfrac{36\pi }{96\pi }=3:8\].

Note: Just remember the formulae of volume , surface area of a cone and a sphere as it will help you a lot in these types of questions. Also be careful while doing calculation as there is a chance that you might make a mistake and take care of the units of the quantity in the above question.
A cone is a three- dimensional geometric shape that tapers smoothly from a flat base ( frequently, though not necessarily, circular) to a point called the apex or vertex.