Question

A conical pit of top diameter \[3.5m\] is \[12m\] deep. What is its capacity in kilolitres?
A) \[38.5{\text{ }}kl\]
B) \[48.5{\text{ }}kl\]
C) \[32.5{\text{ }}kl\]
D) \[28.5{\text{ }}kl\]

Answer 1

Hint: To solve this question, i.e., to find the capacity in kilolitres, we will find the volume of conical pits. For that we will use the formula, $\dfrac{1}{3}\pi {r^2}h,$in the formula we will put, height of conical pit, radius of conical pit using diameter of the conical pit, and hence we will get the value of capacity in kilolitres.

Complete step-by-step answer:
We have been given a conical pit of which it is given that the top diameter is \[3.5m\] and is \[12m\] deep. We need to find its capacity in kilolitres.
We have been given height of conical pit \[ = {\text{ }}h{\text{ }} = {\text{ }}12{\text{ }}m\]
To obtain the radius, we will use the diameter of the conical pit.
Radius of the conical pit \[ = {\text{ }}r{\text{ }} = {\text{ }}\dfrac{{diameter}}{2}\]
\[
  { = {\text{ }}\dfrac{{3.5}}{2}} \\
  { = {\text{ }}1.75{\text{ }}m}
\]
Let us consider the figure of the conical pit.

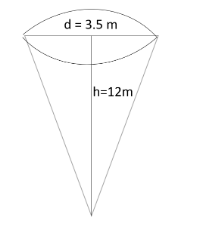
We know that, the capacity of pit \[ = \] volume of cone
$ = \dfrac{1}{3}\pi {r^2}h$
On applying the value in the above formula, we get
$ = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 1.75 \times 1.75 \times 12$
$ = 38.5{m^3}$
$ = 38.5$\[Kiloliters\]
So, capacity of pit is \[38.5{\text{ }}kl.\]
Thus, option (A) \[38.5{\text{ }}kl,\]is correct.
So, the correct answer is “Option A”.

Note: Here, in the question, we have applied the volume formula, when asked about the capacity of the pit, because volume indicates the total amount of space covered by an object in three dimensions and capacity indicates the ability of hold onto something by the object. Volume can be taken of both solid and hollow objects. But capacity can be taken from hollow objects only. And in the question, we have been given the hollow pit. Hence, we have taken volume here.