Question

A cone of maximum volume is carved out of a block of wood of size 20cm × 10cm × 10 cm. Find the volume of the cone carved out, correct to one decimal place.

Answer 1

Hint: A cone of maximum volume which is carved out from a cuboid (wood block) will have the height same as the height of the block and the radius same as half the length of the block. Use this info to find the volume of the cone carved out from the wooden block.

Complete step-by-step answer:
Volume of the cone is $ \dfrac{1}{3}\pi {r^2}h $ , where h is the height of the cone, r is the radius of the base of the cone and the value of $ \pi = \dfrac{{22}}{7} $
We are given that a cone of maximum volume is carved out of a block of wood of size 20cm × 10cm × 10 cm.
We have to find the volume of the carved out cone.

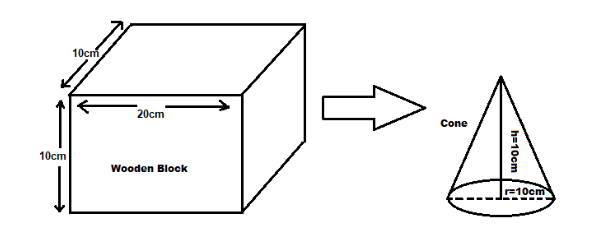
The radius of the newly formed cone will be $ \dfrac{{20}}{2} = 10cm $ , and the height of the cone will be the height of the block which is 10 cm.
 Volume of the cone will be $ \dfrac{1}{3}\pi {r^2}h $ , where r is the radius and h is the height.
 $
\Rightarrow Volum{e_{cone}} = \dfrac{1}{3}\pi {r^2}h \\
\Rightarrow r = 10cm,h = 10cm,\pi = \dfrac{{22}}{7} \\
\Rightarrow Volum{e_{cone}} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {10^2} \times 10 \\
  \therefore Volum{e_{cone}} = 1047.6c{m^3} \\
  $
Volume of the carved out cone is $ 1047.6c{m^3} $

Note: When we put the value of $ \pi $ as 3.14 instead of $ \dfrac{{22}}{7} $ , then we will get a volume which is 0.4 cubic centimeters less than the present obtained volume. Do not confuse a cone with a pyramid, these two are 3-D figures but the difference is the base of the cone is a circle and the base of the pyramid is a polygon. Cone has one vertex whereas a pyramid has more than one vertex.