Question

A cone of height 10 cm and radius 10 cm is to be divided into two parts by cutting through the midpoint of the vertical axis. Then the volume of the conical part is
$
  (a){\text{ }}\dfrac{{100}}{3}\pi c{m^3} \\
  (b){\text{ }}\dfrac{{500}}{3}\pi c{m^3} \\
  (c){\text{ }}\dfrac{{250}}{3}\pi c{m^3} \\
  (d){\text{ }}\dfrac{{125}}{3}\pi c{m^3} \\
 $

Answer 1

Hint: In this question use the concept that overall height of the cone will be divided into two equal parts. Concepts of triangle congruence will help finding the radius at the point where the vertical cut is made. Use the direct formula for the volume of cones to get the answer.

Complete step-by-step answer:

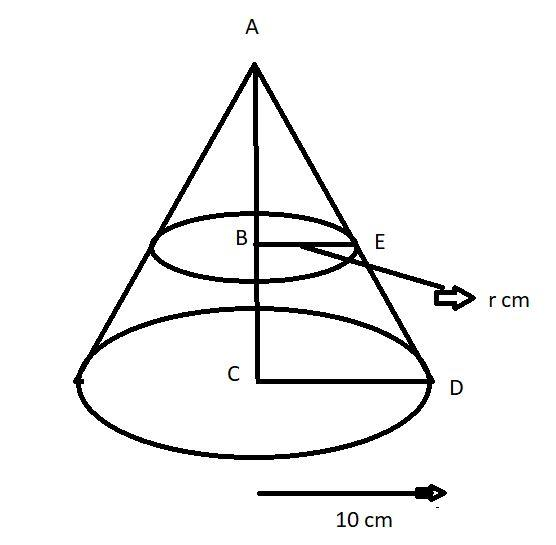
Let us consider the cone as shown in figure the base radius (R) of the cone is 10 cm (see figure.)
Now the cone cut into two parts through the midpoint of its height (at point B see figure).
It is given that the height (h) of the cone is 10 cm
$ \Rightarrow AB = BC = \dfrac{h}{2} = \dfrac{{10}}{2} = 5$ cm.
Let the base radius of the smaller cone is r cm.
$ \Rightarrow BE = r$cm (see figure).
Now the triangle ABE and the triangle ACD is concurrent by the property of angle-angle-angle (AAA).
$ \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CD}}$
Now substitute the values in above equation we have,
$ \Rightarrow \dfrac{{\dfrac{h}{2}}}{h} = \dfrac{r}{{10}}$
On simplifying we get.
$ \Rightarrow r = 5$ cm.
As we know that the volume of the cone is $ = \dfrac{1}{3}\pi {\left( {{\text{radius}}} \right)^2}\left( {{\text{height}}} \right)$
So the volume (${V_1}$) of the upper part of the bigger cone which is also a cone is
$ \Rightarrow {V_1} = \dfrac{1}{3}\pi {\left( {BE} \right)^2}\left( {AB} \right) = \dfrac{1}{3}\pi {\left( r \right)^2}\left( {\dfrac{h}{2}} \right)$…………………. (1)
Now substitute the value in this equation we have,
$ \Rightarrow {V_1} = = \dfrac{1}{3} \times \pi \times {\left( 5 \right)^2}\left( {10} \right)$
Now on simplifying we get,
$ \Rightarrow {V_1} = \dfrac{1}{3} \times \pi \times {\left( 5 \right)^2}\left( {10} \right) = \dfrac{{250}}{3}\pi cm^3$.
So, this is the required answer.
Hence option (C) is correct.

Note: In the lower bottom part which is left after the cutting the midpoint of the vertical axis is the frustum. Congruence of triangle plays a vital role in applying CPCT (corresponding parts of congruent triangles), that helps establishing relations between other sides of the two similar triangles.