Question

A cone is divided into two parts by drawing a plane through a point which divides its height in the ratio \[1:2\] starting from the vertex and the plane is parallel to the base. Compare the volume of the two parts.

Answer 1

Hint: In this question we draw a cone as given that it is divided into two parts by drawing a plane through a point which divides its height in the ratio \[1:2\]. We get a cone at top and a frustum at bottom. By using the formula we will find the volume of cones and volume of frustum. Then we compare the volume of these two parts to get the answer.

Complete step-by-step answer:
Volume of cone $ =\dfrac{1}{3}\pi {{r}^{2}}h $
Volume of frustum $ =\dfrac{\pi h}{3}\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right) $
First we draw a diagram of cone $ ABC $ which is divided into two parts by drawing a plane $ XY $ through a point which divides its height in the ratio \[1:2\] and the plane is parallel to the base as given in the question. Then we get a cone $ ABC $ at the top and a frustum $ XBCY $ at the bottom.

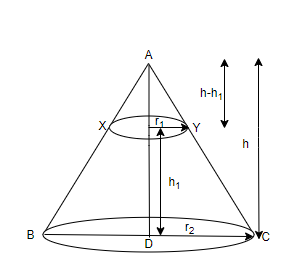
Let the height of the actual cone be $ h $ and height of the cone formed be $ h-{{h}_{1}} $ and the height of the frustum formed be $ {{h}_{1}} $ . Also, let $ {{r}_{1}} $ and $ {{r}_{2}} $ be the radii of the base of the cone and circular section $ XY $ respectively.
Now, as given in the question the height is in the ratio \[1:2\].
So $ \dfrac{h}{{{h}_{1}}}=\dfrac{3}{2} $
When we simplify further we get $ h=\dfrac{3}{2}{{h}_{1}} $
Now we know that the relation between height and radius is given as $ \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{h}{h-{{h}_{1}}} $
When we substitute the value and simplify further we get
\[\begin{align}
  & \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{\dfrac{3}{2}{{h}_{1}}}{\dfrac{3}{2}{{h}_{1}}-{{h}_{1}}} \\
 & \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{\dfrac{3}{2}{{h}_{1}}}{\dfrac{3{{h}_{1}}-2{{h}_{1}}}{2}} \\
 & \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{\dfrac{3}{2}{{h}_{1}}}{\dfrac{1}{2}{{h}_{1}}} \\
 & \dfrac{{{r}_{1}}}{{{r}_{2}}}=3 \\
 & {{r}_{1}}=3{{r}_{2}} \\
\end{align}\]
Now, we know that volume of cone $ =\dfrac{1}{3}\pi {{r}^{2}}h $
So, the volume of cone $ AXY $ will be $ =\dfrac{1}{3}\pi {{r}^{2}}\left( h-{{h}_{1}} \right) $
When we put the value of $ h $ , we get
Volume of cone $ =\dfrac{1}{3}\pi {{r}_{2}}^{2}\left( \dfrac{3}{2}{{h}_{1}}-{{h}_{1}} \right) $
When we simplify further we get
 $ \begin{align}
  & =\dfrac{1}{3}\pi {{r}_{2}}^{2}\left( \dfrac{3{{h}_{1}}-2{{h}_{1}}}{2} \right) \\
 & =\dfrac{1}{6}\pi {{r}_{2}}^{2}{{h}_{1}} \\
\end{align} $
Now as we know that the volume of frustum $ =\dfrac{\pi h}{3}\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right) $
So, the volume of frustum $ XBCY $ will be
  $ \begin{align}
  & =\dfrac{\pi {{h}_{1}}}{3}\left( r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right) \\
 & =\dfrac{\pi {{h}_{1}}}{3}\left( 9r_{2}^{2}+r_{2}^{2}+3{{r}_{2}}{{r}_{2}} \right) \\
 & =\dfrac{\pi {{h}_{1}}}{3}\left( 9r_{2}^{2}+r_{2}^{2}+3{{r}_{2}}^{2} \right) \\
 & =\dfrac{\pi {{h}_{1}}}{3}\left( 13r_{2}^{2} \right) \\
\end{align} $
Now, when we compare the volume of the two parts we get
 $ \begin{align}
  & \dfrac{\text{volume of cone AXY}}{\text{volume of frustum XBCY}}=\dfrac{\dfrac{1}{6}\pi {{r}_{2}}^{2}{{h}_{1}}}{\dfrac{\pi {{h}_{1}}}{3}\left( 13r_{2}^{2} \right)} \\
 & \dfrac{\text{volume of cone AXY}}{\text{volume of frustum XBCY}}=\dfrac{1}{26} \\
\end{align} $
We will get the ratio between volumes of two parts is $ 1:26 $

Note: The key concept to solve this question is to have knowledge about what different shapes are formed when we cut the cone parallel to its base. Also, students should have knowledge about the formula of volume of cone and volume of frustum to solve further. Also, be careful in taking the ratio as given in the question. Remember the formula of cone and frustum, carefully write the terms in the formula. Any misunderstanding while reading the question, students may take the wrong ratio and get different answers.