Question

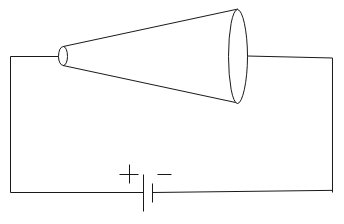
A conductor is made of an isotropic material and has the shape of a truncated cone. A battery of constant emf is connected across it. If at a distance x from the left end, electric field intensity and the rate of generation of heat per unit length are E and H respectively, which of the following graphs are correct?

(A).

(B).

(C).

(D).

Answer 1

Hint: According to the ohm’s law, resistance is the ratio of current and potential difference but resistance also depends on the dimensions of a conductor, it is inversely proportional to the area and hence inversely proportional to the square of length of conductor. The heat depends on the square of current, resistance and time. Current density can also be written as the ratio of electric field inside the conductor and area. Using the above mentioned relations, we can determine the correct graph representations.

Complete answer:

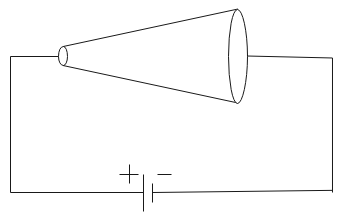
Given a conductor I in the shape of a cone, Therefore, its area is variable. As the battery has a constant emf, the voltage across the conductor as well the current through it is constant. We know that,
$R=\rho \dfrac{l}{A}$
Here, $R$ is the resistance
$\rho $ is the resistivity
$l$ is the length
$A$ is the area of cross section
From the above equation, $R\propto \dfrac{1}{A}$ therefore, as the area increases, the resistance decreases.
The heat generated in a circuit is
$H={{I}^{2}}Rt$
Here, $H$ is the heat generated
$I$ is the current in the circuit
$t$ is the time taken
From the above equation as resistance is inversely proportional to the area, heat and area will be related as .
$\begin{align}
  & H\propto \dfrac{1}{A} \\
 & \Rightarrow H\propto \dfrac{1}{{{x}^{2}}} \\
\end{align}$
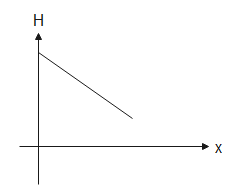
Therefore, the heat is inversely proportional to the square of length.
The current density is given as-
$J=\dfrac{I}{A}$ - (1)
Here, $J$ is the current density and it is the current per unit area.
Current density Is also given as
$J=\dfrac{E}{\rho }$ - (2)
Equating eq (1) and eq (2), we get
$\begin{align}
  & \dfrac{I}{A}=\dfrac{E}{\rho } \\
 & \Rightarrow \dfrac{E}{\rho }=\dfrac{I}{{{x}^{2}}} \\
\end{align}$
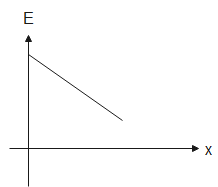
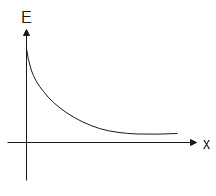
 From the above equation, $E\propto \dfrac{1}{{{x}^{2}}}$
Therefore, the electric field inside the conductor is inversely proportional to the square of length.
Therefore, from the above relations, $H\propto \dfrac{1}{{{x}^{2}}}$ and $E\propto \dfrac{1}{{{x}^{2}}}$.

Hence the correct representations of graphs are (B) and (D).

Note:
The resistivity of a material is its resistance when the length is 1m and the area of the cross section is unity. The resistivity is a constant quantity and is different for different materials. The heat generated in a circuit is dissipated. Unlike current and area, current density is a scalar quantity.