Question

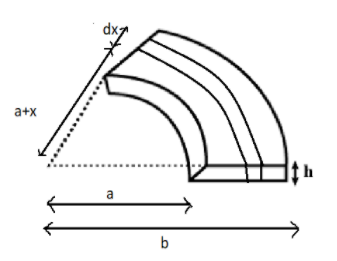
A conductor is in the shape of a quarter of annulus (angular ring) of inner and outer radii $a$and $b$, and thickness $h$. Resistance between the two curved surfaces would be ( $\sigma $= conductance)

Answer 1

Hint: The concept to be used is to find resistance of continuous bodies.
First find the resistance of the Infinite small strip located at $a+x$ distance from the formula of resistance.
Then integrate that infinitesimal strip resistance for the whole body as infinite of such strips can be cut from the given body and all such resistances are arranged in a parallel connection.

Complete step by step answer:
The resistance of a body is obstruction it offers in the path of current.
Resistance of the body in terms of length $l$ ,$A$ area of cross section and $\sigma $ conductance of the body is formulated as
                        $R=\dfrac{l}{\sigma A}$
also $\rho =\dfrac{1}{\sigma }$where$\rho $ is resistivity of the body
Such infinite resistances actually make up the above annular ring so we need to integrate the resistances to find the total resistance.
So, take a strip of length $\partial x$ at a distance $a+x$ from the center.
$\partial R=\dfrac{\partial x}{\sigma A}$
Where area of cross section of strip of width $h$ and length$\dfrac{\pi }{2}\left( a+x \right)$ is $h\dfrac{\pi }{2}\left( a+x \right)$ where $a+x$ is distance of the strip from the centre.
Assuming it subtends $\dfrac{\pi }{2}$ angle at the centre which is constant
Now integrating the equation,
$\Rightarrow \int{\partial R=\int\limits_{a}^{b}{\dfrac{2\partial x}{\sigma \pi \left( a+x \right)h}}}$
$\Rightarrow R=\dfrac{2}{\sigma \pi h}\int\limits_{a}^{b}{\dfrac{\partial x}{\left( a+x \right)}}$
$\Rightarrow R=\dfrac{2}{\sigma \pi h}\left( \log \left( a+x \right) \right)_{a}^{b}$
$\Rightarrow R=\dfrac{2}{\sigma \pi h}\log \left( \dfrac{a+b}{2a} \right)$
This is the total resistance of the annular ring.

Note:
There are many connections in which the resistances can be arranged but two most commonly used are series and parallel connections.
Metals generally are good conductors of current and hence have low resistance to the path of current.
Ohm’s law connecting resistance, voltage and current forms most fundamental law for solving electric circuits