Question

A conducting loop in the shape of a right angled isosceles triangle of height $10\,cm$ is kept such that the ${90^o}$ vertex is very close to an infinitely long conducting wire (see the figure). The wire is electricity insulted from the loop. The hypotenuse of the triangle is parallel to the wire. The current in the triangle loop is in counter clockwise direction and increases at a constant rate of $10\,A\,{s^{ - 1}}$.

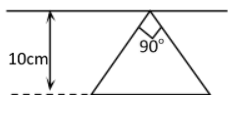
Which of the following statement(s) is (are) true?
(A) The magnitude of induced emf in the wire is $\left( {\dfrac{{{\mu _o}}}{\pi }} \right)volt$
(B) If the loop is rotated at a constant angular speed about the wire, an additional emf of $\left( {\dfrac{{{\mu _o}}}{\pi }} \right)$
(C) The induced current in the wire is in opposite direction to the current along the hypotenuse
(D) There is a repulsive force between the wire and the loop

Answer 1

Hint: When an emf is generated by a change in magnetic flux according to Faraday's Law, the polarity of the induced emf is such that it produces a current whose magnetic field opposes the change which produces it.

Complete step by step answer:
The rate of change of current in the loop is anticlockwise.
$\dfrac{{dI}}{{dt}} = 10\,A/s$

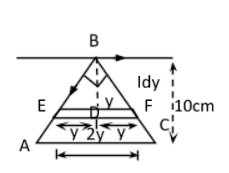
Let take a strip of thickness by at perpendicular distance$Y$. Hence$\Delta \,EDC$ is isosceles triangle hence sides $ED = \,BD\, = Y$
Magnetic flux due to straight wire is
$d\phi = B.dA$ ……………………..(i)
$B$is magnetic field due to straight wire and $dA$is area of strip.
$d\phi = \dfrac{{{\mu _o}I}}{{2\pi y}}(2y.dy)$ ……………………(ii)
$d\phi = \dfrac{{{\mu _o}I}}{\pi }dy$ …………………..(iii)
Integrate equation (iii) w.r.t. limits of ${y_1} = 0$to ${y_2} = 0.1\,m$
$\int {d\phi = \dfrac{{{\mu _o}I}}{\pi }\int_{{y_1} = 0}^{{y_2} = \,0.1m} {dy} } $
$\phi = \dfrac{{{\mu _o}I}}{\pi }\left[ {0.1 - 0} \right]$
$\phi = \dfrac{{{\mu _o}I}}{{10\pi }}$ …………………..(iv)
Differentiate equation (iv) w.r.t. time
$\dfrac{{d\phi }}{{dt}} = \dfrac{{{\mu _o}}}{{10\pi }}\,\dfrac{{dI}}{{dt}}$
\[\dfrac{{d\phi }}{{dt}} = \dfrac{{{\mu _o}}}{\pi }\] $\left[ {\dfrac{{dI}}{{dt}} = 10A/s} \right]$
$E = \dfrac{{{\mu _o}}}{\pi }$
$\left[ {E = \dfrac{{d\phi }}{{dt}}} \right]$

Note:
If current in two parallel wires is in the same direction then they attract each other but if direction is in the opposite direction then they repel each other.