Question

A computer system is advertised with a \[14 - inch\] monitor. The measurement of the monitor is along the diagonal of the screen. The height of the monitor screen is \[9\] inches. What is the width of the monitor screen?

Answer 1

Hint: We have to find the width of the monitor screen. For this, we will consider a triangle formed by length, width and one of the diagonals of the computer monitor. Diagonal is given as \[14\] inches and height is \[9\] inches. We will apply Pythagoras theorem in this triangle and then we will simplify it to find the result.

Complete step by step answer:
Let the computer system be \[ABCD\] where \[BD\] is the diagonal which is \[14\] inches and \[AD\] is the height which is \[9\] inches.

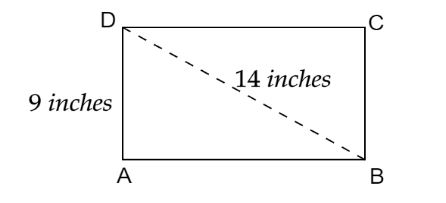
As a computer system monitor is in the form of a rectangle. So, \[\vartriangle ABD\] is a right-angled triangle.We can apply Pythagoras theorem in \[\vartriangle ABD\]. According to the Pythagoras theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides of the triangle. So, we can write,
\[ \Rightarrow B{D^2} = A{B^2} + A{D^2}\]
Putting the values, we get
\[ \Rightarrow {\left( {14} \right)^2} = A{B^2} + {\left( 9 \right)^2}\]
On simplifying, we get
\[ \Rightarrow 196 = A{B^2} + 81\]

Subtracting \[81\] from both the sides, we get
\[ \Rightarrow 115 = A{B^2}\]
On rewriting, we get
\[ \Rightarrow A{B^2} = 115\]
Taking square root both sides, we get
\[ \Rightarrow AB = \pm \sqrt {115} \]
But length can’t be negative. So, \[AB = \pm \sqrt {115} \].
Therefore, we get
\[ \Rightarrow AB = \sqrt {115} \]
On calculating, we get
\[ \therefore AB = 10.724\]

Therefore, the width of the monitor screen is \[10.724\] inches.

Note: Here, we have taken any general computer monitor that is rectangular in shape, which allowed us to apply the Pythagoras theorem. For any right-angle triangle, Pythagoras theorem is the most important formula. Since, diagonals of a rectangle are equal in length, we can take any one diagonal and two adjacent sides to apply Pythagoras theorem.