Question

A compound microscope is having an objective of focal length $4mm$ and an eyepiece of focal length $25mm$. The objective develops a real image at a distance of $180mm$. If the eye-piece is kept in a normal adjustment, then the magnification will be
$\begin{align}
  & A.45 \\
 & B.90 \\
 & C.225 \\
 & D.440 \\
\end{align}$

Answer 1

Hint: The magnification of the mentioned set up in the question is given as the product of the ratio of the distance of the image produced by the eyepiece to the distance of the image produced by the objective lens and the ratio of the distance of the distinct vision to the focal length of the eyepiece plus one. This will help you in solving this question.

Complete step by step answer:
It has been mentioned in the question that the focal length of the objective lens is given as,
${{f}_{o}}=4mm$
And the focal length of the eyepiece lens is given as,
${{f}_{e}}=25mm$
The distance of the image of the objective lens is given as,
${{v}_{o}}=180mm$
The magnification of this system of arrangement can be found using the equation,
${{M}_{D}}=\dfrac{{{v}_{e}}}{{{v}_{o}}}\left[ 1+\dfrac{D}{{{f}_{e}}} \right]$
Where $D$ be the distance of the distinct vision and ${{v}_{e}}$ be the image distance of the eyepiece lens.
According to the lens equation, we can write that,
$\dfrac{1}{{{v}_{e}}}-\dfrac{1}{{{v}_{o}}}=\dfrac{1}{{{f}_{o}}}$
Substituting the values in it will give,
$\dfrac{1}{180}-\dfrac{1}{{{v}_{o}}}=\dfrac{1}{4}$
Rearranging the equation in terms of ${{v}_{o}}$will be written as,
$\dfrac{1}{{{v}_{o}}}=\dfrac{11}{45}$
This can be substituted in the equation of magnification,
That is,
\[{{M}_{D}}=\dfrac{180\times 11}{45}\left[ 1+\dfrac{25\times {{10}^{-2}}}{25\times {{10}^{-3}}} \right]\]
Simplifying this equation will give,
\[{{M}_{D}}=44\times 10=440\]

Therefore the answer has been given as option D.

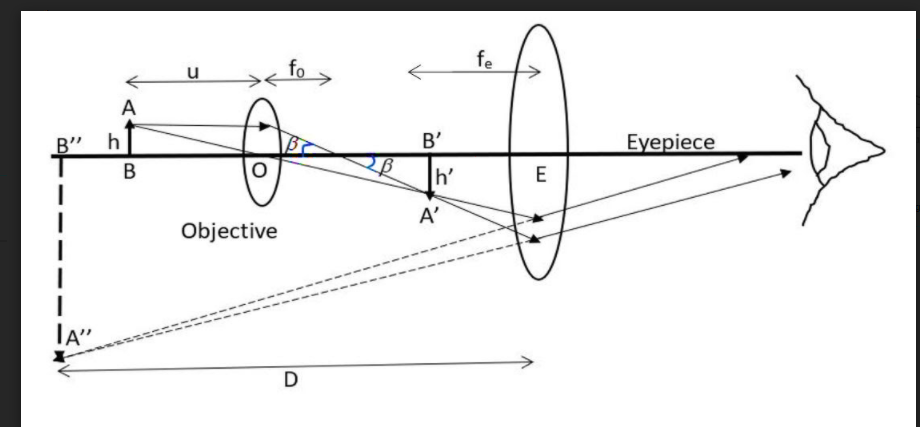
Note:
The distance of distinct vision is the reference distance in order to see the image clearly or comfortably. The distance shorter than this will give a blurred image which will affect our vision. In other words, this is the minimum distance between the object and the human eye for the distinct vision.