Question

A compound is made up of atoms A and B. Atoms A are present at the corners of the cube as well as at the center of each face while atoms B are present at \[50%\] of octahedral voids and \[~25%\] tetrahedral voids. If the crystal cuts in such a way that all face centered atoms from one of the axes are removed the new formula of the compound is:
A.\[AB\]
B.${{A}_{4}}{{B}_{3}}$
C.${{A}_{2}}{{B}_{4}}$
D.${{A}_{2}}{{B}_{3}}$

Answer 1

Hint: We know that the relation between the tetrahedral void and octahedral void is that the tetrahedral void is two times of octahedral void. The simplest formula of the compound in the given crystal is determined by calculating the ratio of $\alpha :\beta .$

Complete answer:
As we know that the solid crystal is arranged in a three-dimensional order where each atom which is considered as a sphere is packed and voids are formed. Two types of voids are formed, tetrahedral and octahedral. The tetrahedral voids are formed when four atoms are arranged in tetrahedral like shape, the void or we can say the space between them is tetrahedral void while when atoms are arranged in octahedral order they form an octahedral void. A unit cell is a small portion of crystal lattice, like as we have in a rhombic cube. In a rhombic cube one small colored portion can be considered as a unit cell. So, there are some modes in which atoms are arranged in a unit cell, SCC BCC and FCC. In a simple cubic cell eight atoms are present at the corners while in the other two there are some extra atoms. In BCC eight atoms are at the corner and one atom is present at the center. In FCC there are eight atoms at the corners and one at each face.

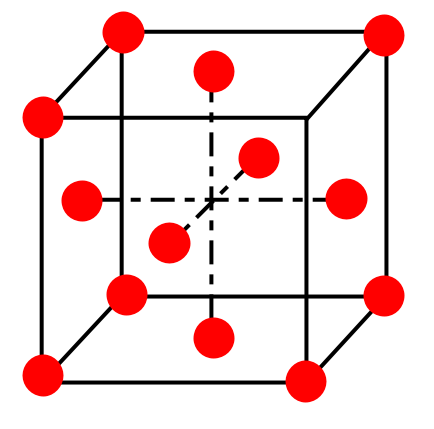
The face centered cube which has a present at corners and at each face. The total number of atoms contributed by corners $=\dfrac{8}{8}\alpha =\alpha ,$ and F.C.C. total number of atoms contributed by faces $=\dfrac{6}{2}\alpha =3\alpha .$
$\therefore $ The total number of ‘A’ atoms $=\alpha +3\alpha \Rightarrow 4\alpha .$
Likewise, the number of octahedral voids $N=4,$ and the number of tetrahedral voids $=2N=2\times 4=8$ where N is the number of atoms present per unit cell.
Since $50%$ of octahedral voids $4\times \dfrac{50}{100}=2\beta ,$ and $25%$of tetrahedral voids $8\times \dfrac{25}{100}=2\beta .$
$\therefore $ The total number of ‘B’ atoms \[=2\beta +2\beta \Rightarrow 4\beta .\]
Thus, the new formula of the compound is $4\alpha +4\beta \Rightarrow 4\alpha \beta \approx \alpha \beta $
Therefore, the correct answer is option A.

Note:
Remember that the type of arrangement will decide the number of voids in a unit cell. As we have FCC face centered unit cells. In this unit cell we have overall four atoms, which means there will be four octahedral voids while the tetrahedral voids are doubled in number.