Question

A compass needle free to turn in a horizontal plane is placed at the centre of a circular coil of 30 turns and radius 12 cm. The coil is in a vertical plane making an angle of \[{{45}^{0}}\] with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
(a) Determine the horizontal component of the earth’s magnetic field at the location.
(b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of \[{{90}^{0}}\] in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.

Answer 1

Hint: There will be a magnetic field produced by this circular coil at the centre. A coil which has some number of turns, radius and current in it. This will help us to determine the horizontal component of earth’s magnetic field at the location.

Formula used:
Magnetic field at the centre of the coil:
\[B=\dfrac{{{\mu }_{0}}NI}{2R}\]
Horizontal component of earth’s magnetic field is given by:
\[H=B\cos \theta \]
Where, \[\theta =\text{angle of dip}\]

Complete step by step answer:
Here, we are given a magnetic needle placed at the centre of a circular coil. Information about circular coil:
Number of turns, \[N=30\]
Radius of the coil, \[R=12cm=12\times {{10}^{-2}}m\]
Current in the coil, \[I=0.35A\]
Now, magnetic field at the centre of the coil is given by:
\[\begin{align}
  & B=\dfrac{{{\mu }_{0}}NI}{2R} \\
 & \Rightarrow B=\dfrac{4\pi \times {{10}^{-7}}\times 30\times 0.35}{2\times 12\times {{10}^{-2}}} \\
 & \Rightarrow B=5.5\times {{10}^{-5}}T \\
\end{align}\]
Magnetic field due to the coil is found to be \[B=5.5\times {{10}^{-5}}T\].
(a) Now, we will determine the horizontal component at centre of the coil, having angle of dip or angle of inclination \[{{45}^{0}}\] .

We know that horizontal component is given by the formula,
\[H=B\cos \theta \]
Then,
\[\begin{align}
  & H=B\cos \theta \\
 & \Rightarrow H=5.5\times {{10}^{-5}}\times \cos {{45}^{0}} \\
 & \Rightarrow H=5.5\times {{10}^{-5}}\times \dfrac{1}{\sqrt{2}} \\
 & \Rightarrow H=3.9\times {{10}^{-5}}T \\
\end{align}\]
Hence, the horizontal component of Earth’s magnetic field at that location is \[3.9\times {{10}^{-5}}T\].
(b) Now, the direction of current in the coil is reversed and the coil is rotated through \[{{90}^{0}}\] anticlockwise. i.e.
  

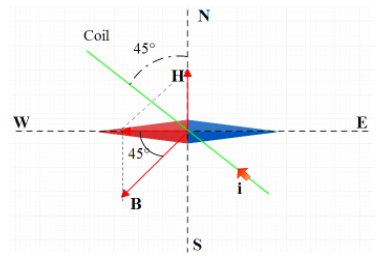
So, by changing the direction of current and position of the coil, the direction of the magnetic field is also rotated \[{{90}^{0}}\] in clockwise direction to the previous one.
Now, the value of H remains unchanged. But the needle points from east to west.

Note:
While doing calculation or putting any given value in the formula just remember to change the units of quantity to SI units to get the required correct result. To solve these types of questions, we must have the proper idea how to calculate the horizontal and vertical components of earth’s magnetic field and must not be confused about the value of \[\theta =\text{angle of dip}\].