Question

A combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2ohm, the resistance of the combination is:
A.$2.5\Omega $
B. $3\Omega $
C.$1.5\Omega $
D. $5\Omega $

Answer 1

Hint: As a first step, you could make a neat diagram of the given combination of resistors. Then you could identify the connections made in series as well as in parallel to result in that combination. Now you could thus simplify the complex combination into a simple series and parallel combination and find the effective resistance.

Formula used:
Effective resistance for series connection,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$
Effective resistance for parallel connection,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+\dfrac{1}{{{R}_{4}}}$

Complete answer:
In the question, we are asked to find the effective resistance of the given combination of resistors. So we are given a total of 12 resistors placed in certain combinations of both parallel as well as series connections.
We have four sets of series combinations of three resistors. We are also given the value of each resistor as $2\Omega $. So the connection can be depicted as shown below.

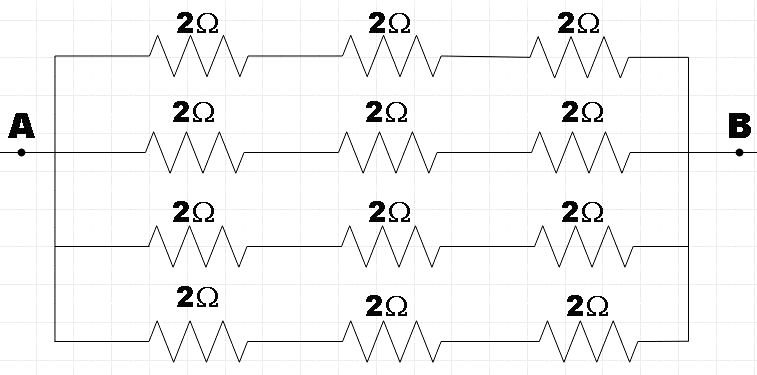
So we are asked to find the effective resistance across A and B.
Firstly let us find the effective resistance of the series connection of three resistors of each $2\Omega $.
We know that for a series connection, the effective resistance is given by the sum of the resistances of all the resistors connected in series. That is,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$
Substituting the values of resistances, the effective resistance of each set will be,
${{R}_{eff}}=2+2+2=6\Omega $
But we have four such sets connected parallel. We know that, for parallel connection, the effective resistance is given by,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+\dfrac{1}{{{R}_{4}}}$
Substituting the effective resistance of $6\Omega $ for each set, we get,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}$
$\Rightarrow \dfrac{1}{{{R}_{eff}}}=\dfrac{4}{6}$
$\therefore {{R}_{eff}}=\dfrac{6}{4}=1.5\Omega $
So, we found the effective resistance of the given combination to be$1.5\Omega $.

Hence, option C is found to be the right answer.

Note:
For the questions in which we are asked to find the effective resistance, you could firstly simplify the combination into series and parallel connections. Sometimes, you may find other simplifications when we find Wheatstone bridge combinations. We could then find the effective resistance for simple series and parallel connections and hence the effective resistance of the combination.