Question

A collision of two blocks takes place along a horizontal surface without friction. First block with mass ${{M}_{1}}=3.00kg$ initially moves to the left with speed ${{V}_{1}}=5.00m/s$ when a hits a block ${{M}_{2}}=5.00kg$ initially moving to the right with speed ${{V}_{2}}=2.00m/s$. After colliding, the block with mass ${{M}_{1}}$ is moving to the right with speed $1m/s$.Which of the blocks underwent a larger magnitude of acceleration during the collision.
a) The block with mass ${{M}_{1}}$
b) The block with mass ${{M}_{2}}$
c) The magnitude of acceleration was same for both the blocks
d) More information about the time of collision is required to answer the question

Answer 1

Hint: It is given in the question the two blocks are moving towards each other along a frictionless surface. Hence the blocks will collide with each other resulting in a collision. It is given that the blocks move in opposite directions after the collision. Hence we can find the initial and the final velocities of both the blocks using law of conservation of momentum. Since the time of collision is the same for both the masses, we can conclude that the mass having greater change in velocity i.e. before and after the collision will undergo greater acceleration due to collision.

Complete answer:
Let us say a body of mass m moves with a velocity v. Hence the momentum (P)of the body is given as the product of its mass and the velocity i.e. $P=\text{mv kgm}{{\text{s}}^{\text{-1}}}$.

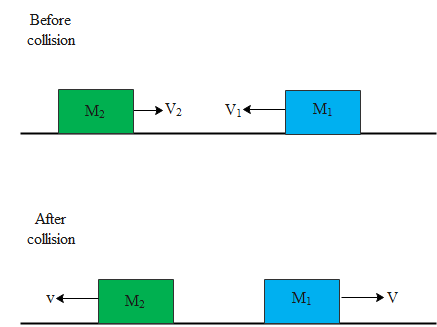
In the above diagram we can see that the blocks are approaching towards each other and after collision move away from each other. Let us take the velocities along the left direction to be positive and along the right to be negative. Hence by law of conservation of momentum we get,
$\begin{align}
  & \text{Initial momentum=Final momentum} \\
 & {{\text{M}}_{\text{1}}}{{V}_{1}}+{{\text{M}}_{2}}\left( -{{V}_{2}} \right)={{\text{M}}_{\text{1}}}\left( -V \right)+{{\text{M}}_{2}}v \\
 & {{\text{M}}_{\text{1}}}{{V}_{1}}-{{\text{M}}_{2}}{{V}_{2}}=-{{\text{M}}_{\text{1}}}V+{{\text{M}}_{2}}v \\
\end{align}$
After substituting all the information given to us in the question in the above equation the final velocity (v)of the block with mass ${{M}_{2}}$we get,
$\begin{align}
  & {{\text{M}}_{\text{1}}}{{V}_{1}}-{{\text{M}}_{2}}{{V}_{2}}=-{{\text{M}}_{\text{1}}}V+{{\text{M}}_{2}}v \\
 & 3\times 5-5\times 2=-3\times 1+5\left( v \right) \\
 & 15-10=-3+5\left( v \right) \\
 & 5\left( v \right)=5+3 \\
 & v=\dfrac{8}{5}m{{s}^{-1}}=1.6m{{s}^{-1}} \\
\end{align}$
The change in velocity of block with mass ${{M}_{1}}$is,
${{V}_{1}}-V=\Delta V=1-5=-4m{{s}^{-1}}$, whereas the change in velocity of the block with mass ${{M}_{2}}$is,
${{V}_{2}}-v=\Delta v=1.6-2=-0.4m{{s}^{-1}}$.
Since for both the blocks, the time of collision is the same we can conclude that the rate in change of velocity with time i.e. acceleration, for the block with mass ${{M}_{1}}$ is greater than the block with mass ${{M}_{2}}$.

Hence the correct answer is option a.

Note:
In the above solution we can see that the change in velocity with time is negative. It means that the velocity of both the blocks have decreased after collision. Hence we can say that both the blocks have undergone deceleration. The surface along which the blocks are moving is considered to be frictionless, hence there is no loss of momentum of the bodies while moving before collision.