Question

A college awarded 38 medals in Football, 15 in Basketball and 20 to Cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports?

Answer 1

Hint: Assign the number of men winning medals in three sports into three different sets. Generate the conditions given in the question into set operations and use the formulae of set theory like \[\text{n}\left( \text{A}\bigcup{\text{B}\bigcup{\text{C}}} \right)\text{ = n}\left( \text{A} \right)\text{ + n}\left( \text{B} \right)\text{ + n}\left( \text{C} \right)\text{ }-\text{ n(A}\bigcap{\text{B) }-\text{ n}\left( \text{B}\bigcap{\text{C}} \right)\text{ }-\text{ n}\left( \text{C}\bigcap{\text{A}} \right)\text{ + n}\left( \text{A}\bigcap{\text{B}\bigcap{\text{C}}} \right)}\]to find out the actual answer. Here, $\text{n}\left( \cdot \right)$represents the number of elements in a set.

Complete step by step answer:
Let, the men winning medals in Football constitute the set F, those winning medals in Basketball constitute set B and those winning in Cricket constitute the set C.

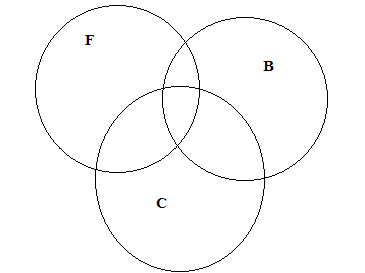
It is given that, n(F) = 38, n(B) = 15 and n(C) = 20.
Now, there are a total number of 58 men who received combinedly in the three sports.
Hence, we can write $\text{n}\left( \text{F}\bigcup{\text{B}\bigcup{\text{C}}} \right)\text{ = 58}$. 3 men won simultaneously in all the three sports. Thus, it can be expressed as $\text{n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ = 3}$.
Now putting these values in the formula,
\[\begin{align}
  & \text{n}\left( \text{F}\bigcup{\text{B}\bigcup{\text{C}}} \right)\text{ = n}\left( \text{F} \right)\text{ + n}\left( \text{B} \right)\text{ + n}\left( \text{C} \right)\text{ }-\text{ n(F}\bigcap{\text{B) }-\text{ n}\left( \text{B}\bigcap{\text{C}} \right)\text{ }-\text{ n}\left( \text{C}\bigcap{\text{F}} \right)\text{ + n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)} \\
 & \Rightarrow \text{ 58 = 38 + 15 +20 }-\text{ n(F}\bigcap{\text{B) }-\text{ n}\left( \text{B}\bigcap{\text{C}} \right)\text{ }-\text{ n}\left( \text{C}\bigcap{\text{F}} \right)\text{ +}}\text{ 3} \\
 & \Rightarrow \text{ n(F}\bigcap{\text{B) + n}\left( \text{B}\bigcap{\text{C}} \right)\text{ + n}\left( \text{C}\bigcap{\text{F}} \right)\text{ = 76 - 58 = 18 }....\text{(i)}} \\
\end{align}\]
To find out the number of men winning medals in exactly two of the three sports, we need to find out $\text{n}\left( \text{F}\bigcap{\text{B}\bigcap{{{\text{C}}^{c}}}} \right)\text{ + n}\left( \text{F}\bigcap{{{\text{B}}^{c}}\bigcap{\text{C}}} \right)\text{ + n}\left( {{\text{F}}^{c}}\bigcap{\text{B}\bigcap{\text{C}}} \right)$.
We know the formula,
$\text{n}\left( \text{A}\bigcap{\text{B}} \right)\text{ = n}\left( \text{A}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + n}\left( \text{A}{{\bigcap{\text{B}\bigcap{\text{C}}}}^{c}} \right)$
Applying this formula in equation (i), we get,
$\begin{align}
  & \text{n}\left( \text{F}\bigcap{\text{B}} \right)\text{ + n}\left( \text{B}\bigcap{\text{C}} \right)\text{ + n}\left( \text{C}\bigcap{\text{F}} \right)\text{ = 18} \\
 & \Rightarrow \text{ n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + n}\left( \text{F}\bigcap{\text{B}\bigcap{{{\text{C}}^{c}}}} \right)\text{ + n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + n}\left( {{\text{F}}^{c}}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + n}\left( \text{F}\bigcap{{{\text{B}}^{c}}\bigcap{\text{C}}} \right)\text{ = 18} \\
 & \Rightarrow \text{ n}\left( \text{F}\bigcap{\text{B}\bigcap{{{\text{C}}^{c}}}} \right)\text{ + n}\left( \text{F}\bigcap{{{\text{B}}^{c}}\bigcap{\text{C}}} \right)\text{ + n}\left( {{\text{F}}^{c}}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + 3*n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ = 18} \\
\end{align}$Putting $\text{n}\left( \text{F}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ = 3}$in the above equation, we get,
$\begin{align}
  & \text{ n}\left( \text{F}\bigcap{\text{B}\bigcap{{{\text{C}}^{c}}}} \right)\text{ + n}\left( \text{F}\bigcap{{{\text{B}}^{c}}\bigcap{\text{C}}} \right)\text{ + n}\left( {{\text{F}}^{c}}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ + 9 = 18} \\
 & \therefore \text{ n}\left( \text{F}\bigcap{\text{B}\bigcap{{{\text{C}}^{c}}}} \right)\text{ + n}\left( \text{F}\bigcap{{{\text{B}}^{c}}\bigcap{\text{C}}} \right)\text{ + n}\left( {{\text{F}}^{c}}\bigcap{\text{B}\bigcap{\text{C}}} \right)\text{ }=\text{ 9} \\
\end{align}$
Thus, 9 men have won medals in exactly two of the three sports in the college.
Note: If n(A) is the number of elements in the set A, then $\text{n}\left( {{\text{A}}^{c}} \right)$is the number of elements in the universal set, other than those elements present in set A. It is also important to remember the various formulae about the union and intersection of sets. Otherwise, the equations become unsolvable.