Question

A coil possessing both inductance L and resistance R is connected to a $24V$ dc supply having negligible internal resistance. The dc current in this circuit is found to be $3A$. When the coil is connected to a $24V$, $50Hz$ ac supply, the circuit current is found to be $0.8A$ . Find:
(a) the resistance of the coil.
(b) the inductance of the coil.

Answer 1

Hint: This question utilizes the concept of Circuits. We know that the inductor does not work on a dc circuit, thus we can find resistance from there. Then we can use this value in the case of ac circuit and find out the inductance

Formulae used:
\[{I_{DC}} = \dfrac{{{V_{DC}}}}{R}\]
where ${I_{DC}}$ is the current in the circuit, ${V_{DC}}$ is the voltage and $R$ is the resistance of the coil.
${Z^2} = {R^2} + {X_L}^2$
where $Z$ is the impedance, $R$ is the resistance and ${X_L}$ is the inductive reactance.
${X_L} = \omega L = 2\pi fL$
where $\omega $ is the angular frequency, $f$ is the frequency of the ac circuit and $L$ is the inductance.

Complete step by step answer:
As we are considering inductance $L$ and resistance $R$ of the same coil, it becomes a series $LR$ circuit. Now we have two cases-
(a) $24V$ dc supply connected. Inductance does not play any role in dc source. Thus, the circuit has resistance $R$

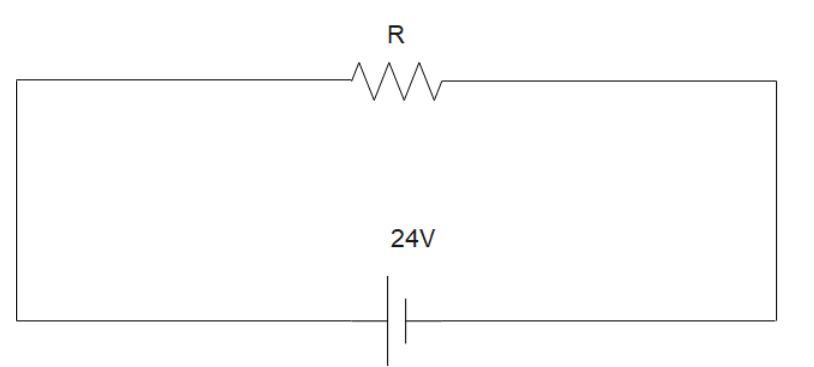
Now, the current in the coil is given by
\[{I_{DC}} = \dfrac{{{V_{DC}}}}{R}\]
where ${I_{DC}}$ is the current in the circuit, ${V_{DC}}$ is the voltage and $R$ is the resistance of the coil.
 Inserting given values we get
\[\Rightarrow 3 = \dfrac{{24}}{R} \\
\Rightarrow R = \dfrac{{24}}{3} \\
\Rightarrow R = 8\Omega \\ \]
(b) $24V$ , $50Hz$ ac supply connected to the circuit with Resistance $R$ and inductance $L$

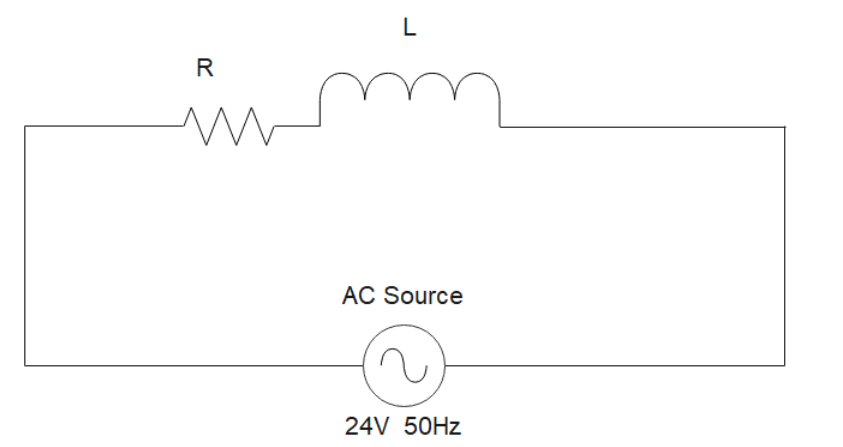
Now, we find circuit impedance using the formula ${Z^2} = {R^2} + {X_L}^2$ where $Z$ is the impedance, $R$ is the resistance and ${X_L}$ is the inductive reactance.
$ \Rightarrow {Z^2} = {R^2} + {X_L}^2$ ---------------(i)
We know that ${X_L} = \omega L = 2\pi fL$ where $\omega $ is the angular frequency, $f$ is the frequency of the ac circuit and $L$ is the inductance
Thus, we have eq (i) as
$ \Rightarrow {Z^2} = {R^2} + {\left( {2\pi fL} \right)^2}$
$ \Rightarrow Z = \sqrt {{R^2} + {{\left( {2\pi fL} \right)}^2}} $ ---------------(ii)
Now, for ac circuits
$ \Rightarrow {I_{AC}} = \dfrac{{{V_{AC}}}}{Z}$
Substituting from eq (ii), we get
$ \Rightarrow {I_{AC}} = \dfrac{{{V_{AC}}}}{{\sqrt {{R^2} + {{\left( {2\pi fL} \right)}^2}} }}$

Inserting values from the question, we get
$ \Rightarrow 0.8 = \dfrac{{24}}{{\sqrt {{8^2} + {{\left( {2\pi \times 50 \times L} \right)}^2}} }}$
Squaring both the sides and rearranging, we get
$\Rightarrow {8^2} + {\left( {2\pi \times 50 \times L} \right)^2} = \dfrac{{{{\left( {24} \right)}^2}}}{{{{\left( {0.8} \right)}^2}}} \\
\Rightarrow {\left( {2\pi \times 50 \times L} \right)^2} = \dfrac{{{{\left( {24} \right)}^2}}}{{{{\left( {0.8} \right)}^2}}} - {8^2} \\
\Rightarrow {\left( {2\pi \times 50 \times L} \right)^2} = 836 \\
\Rightarrow 2\pi \times 50 \times L = \sqrt {836} \\
\Rightarrow L = \dfrac{{\sqrt {836} }}{{100\pi }} \\ $
$\therefore L = 0.9\,H$

Therefore, the resistance of the coil is $8\Omega $ and inductance is $0.9H$.

Note:Here, $H$ is the unit of inductance called Henry. Students should be careful not to mix up ${X_L}$ and$L$ . The first one of them is inductive reactance, whereas the second one is inductance. Mixing up the two will result in the wrong answer.