Question

A coil of radius $R$ carries current ${i_1}$. Another concentric coil of radius \[r(r \ll R)\] carries current ${i_2}$. Places of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. If the maximum kinetic energy of smaller coil when both are released is $\dfrac{{{\mu _0}{i_1}{i_2}\pi r_{}^2MR}}{{X\left( {MR_{}^2 + mr_{}^2} \right)}}$. Find $X$?
Masses of coils are $M$ and $m$, respectively.

Answer 1

Hint: To solve this question think about the conservation of the angular momentum. By finding the inertia, angular velocity, potential energy we are able to find the solution for this question.

Formula used:
\[{I_1}{\omega _1}{\text{ = }}{I_2}{\omega _2}\]
\[\dfrac{1}{2}{I_1}\omega _1^2 + \dfrac{1}{2}{I_2}\omega _2^2 = U\]
$U = MB\cos \theta $

Complete step by step answer:
We can find the solutions by understanding the laws of conservation of angular momentum and energy.
The law of conservation of energy states that the energy can be neither created nor can it be destroyed.
Given that a coil of radius $R$ carries current ${i_1}$ and another concentric coil of radius \[r(r \ll R)\] carries current ${i_2}$. The Mass of the coil with radius $R$ is $M$ and mass of the coil with radius $r$ is $m$.
Also, places of two coils are mutually perpendicular and both the coils are free to rotate about common diameter as shown in the diagram.

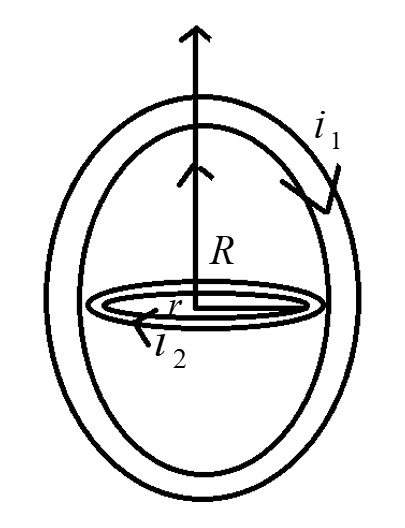
The magnetic induction at centre due to current in larger coil, $B = \dfrac{{{\mu _0}{i_1}}}{{2R}}{\mu _ \circ }$
Where
$B$ is the magnetic induction.
${\mu _ \circ }$is the permeability of free space.
$R$ is the radius
Also, magnetic moment is given as $M = I \times A$
Where,
$M$ is the magnetic moment
$I$ is the current
Hence for smaller coil magnetic moment $M = \pi r_{}^2{i_2}$
Initially when the coils are perpendicular to each other the angle between $M$ and $B$ is ${90^ \circ }$ hence potential energy is given as
${U_1} = - MB\cos {90^ \circ } = 0$
When the coils become coplanar the angle between $M$ and $B$ is ${0^ \circ }$ hence potential energy U2 is given as
${U_2} = - MB\cos {0^ \circ } = - MB$
Therefore, decrease in the potential energy, $U = {U_1} - {U_2}$
\[ \Rightarrow U = 0 - ( - MB)\]
\[ \Rightarrow U = MB = \dfrac{{{\mu _0}{i_1}{i_2}\pi r_{}^2}}{{2R}}\]
This decrease in potential energy is converted into kinetic energy.
Also, kinetic energy becomes maximum when the coils are coplanar.
Let \[{\omega _1}\] and \[{\omega _2}\]be angular velocity and ${I_1}$ ${I_2}$ be the moment of inertia of larger and smaller coil respectively when the coils become coplanar.
Also ${I_1} = MR_{}^2$and \[{I_2} = mr_{}^2\]
According to law of conservation of angular momentum \[{I_1}{\omega _1}{\text{ = }}{I_2}{\omega _2}\]
Hence we have ${\omega _1} = \dfrac{{{I_2}{\omega _2}}}{{{I_1}}}$
Also, kinetic energy of rotating body is given as \[\dfrac{1}{2}{I_{}}\omega _{}^2\]
Hence, according to law of conservation of energy,
\[ \Rightarrow \dfrac{1}{2}{I_1}\omega _1^2 + \dfrac{1}{2}{I_2}\omega _2^2 = U\]
Using the value ${\omega _1} = \dfrac{{{I_2}{\omega _2}}}{{{I_1}}}$
We have,
\[ \Rightarrow \dfrac{1}{2}{I_1}\left( {\dfrac{{{I_2}{\omega _2}}}{{{I_1}}}} \right)_{}^2 + \dfrac{1}{2}{I_2}\omega _2^2 = U\]
$ \Rightarrow U = \dfrac{1}{2}{I_1}\omega _2^2\left( {\dfrac{{{I_1}}}{{{I_2}}} + 1} \right)$
$ \Rightarrow \dfrac{1}{2}{I_1}\omega _2^2 = \dfrac{{U{I_1}}}{{{I_1} + {I_2}}}$
By substituting the values for $U$, ${I_1}$ and ${I_2}$ we get,
\[ \Rightarrow \dfrac{1}{2}{I_1}\omega _2^2 = \dfrac{{{\mu _o}{i_1}{i_2}\pi r_{}^2MR}}{{2(MR_{}^2 + mr_{}^2)}} \]
Where kinetic energy is \[\dfrac{1}{2}{I_1}\omega _2^2\]
By comparing the equations $\dfrac{{{\mu _0}{i_1}{i_2}\pi r_{}^2MR}}{{X\left( {MR_{}^2 + mr_{}^2} \right)}}$ and \[\dfrac{{{\mu _o}{i_1}{i_2}\pi r_{}^2MR}}{{2(MR_{}^2 + mr_{}^2)}}\] we get $X = 2$

Therefore $X = 2$ is the required answer.

Note:
The law of conservation of angular momentum states that there will be no change in the angular momentum that occurs if no external torque is acting on it. The negative sign in the potential energy $U$ indicates that both the coils are moving in the direction opposite to each other.