Question

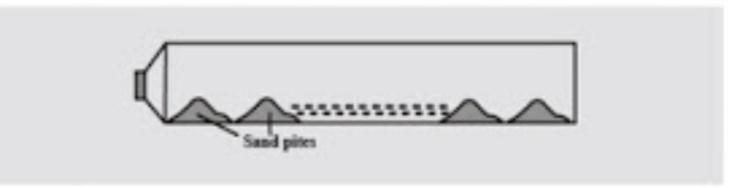
A closed pipe of the length 300cm contains some sand. A speaker is connected at one of its ends. The frequency of the speaker at which the sand will arrange itself in 20 equidistant piles is close to (velocity of the sound is 300m/s).

A. 10kHz
B. 5kHz
C. 1kHz
D. 100kHz

Answer 1

Hint: We know that the number of waves will be half of the number of equidistant piles of sand. Also we have to use the basic relation between frequency, wavelength and velocity. Also we can relate this closed pipe with properties of closed organ pipe.

Complete step-by-step answer:
Here, the total length of pipe will be divided into 20 equidistant piles of sand. These piles will be divided by 10 equal wavelengths.
Since, sand lies on the surface of the bottle, when we divide it into 20 equal parts then only 20 crests of wavelength forms. Hence the length of pipe gets divided into 10 equal wavelengths.
So, relation between the length of the pipe and the equal wavelengths given by,
${\text{L}} = 10\lambda $
Where,
L= length of the closed organ pipe
$\lambda $= equal wavelengths
Here given L= 300 cm or 3m
On putting value in equation we have
$3{\text{m}} = 10\lambda $
On further solving we get
$\lambda $=0.3m
Now, we use basic relation between wavelength, velocity and frequency which is given by
$f = \dfrac{v}{\lambda }$
Where
 f = frequency
$\lambda $= wavelength
v= velocity of wave
On putting the values v= 300ms$^{-1}$ and $\lambda $=0.3m we get
$f = \dfrac{{300}}{{0.3}}Hz$
$f = 1000Hz$
Finally we get
$f = 1kHz$
$\therefore $ Option (C) is correct.

Note: Be careful while using the concept of closed organ pipe means be cautious while dividing wavelength in the pipe into equal parts. The length of pipe will be divided into 10 equal parts not into 20. For open organ pipe the different relation between wavelength and length of the pipe is different from closed organ pipe.