Question

A class has 175 students, The following description gives the number of students studying one or more of the subjects in this class: Mathematics 100, physics 70, chemistry 46, Mathematics and physics 30, mathematics and chemistry 28, physics and chemistry 23, mathematics, physics and chemistry 18. How many students are enrolled in mathematics alone, physics alone and children alone? Are there students who have not offered any of these subjects?

Answer 1

Hint: In this question, we are given data for a class of 175 students. There are three subjects: mathematics, physics and chemistry. Every subject is studied by a given number of students. Some students are studying two subjects while some are studying all the three subjects. We have to find the number of students studying a single subject alone using set theory. We also have to find the number of students who are studying none of the above three subjects.

Complete step by step solution:
Now, let’s discuss the solution.
Here, we are given a class of 175 students. The data is provided of the students who are studying the subjects: mathematics, physics and chemistry. Data is given as follows:
Number of students who study Mathematics = n(M) = 100
Number of students who study Physics = n(P) = 90
Number of students who study Chemistry = n(C) = 46
Number of students who study both Mathematics and Physics = n($M\cap P$) = 30
Number of students who study both Mathematics and Chemistry = n($M\cap C$) = 28
Number of students who study both Physics and Chemistry = n($P\cap C$) = 23
Number of students who study all the three subjects = n($M\cap P\cap C$) = 18
Now, let’s represent all the given data on a venn diagram so that it becomes easy to find the solution.

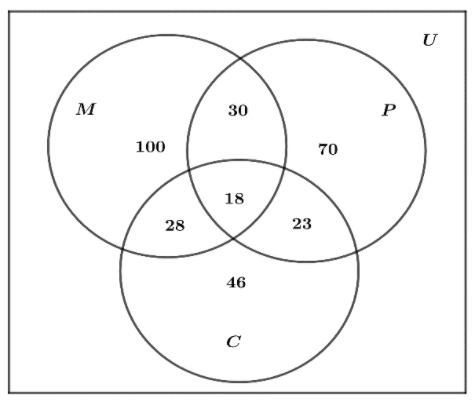
In question it asked to find the number of students in each particular subject alone so will use a formula:
N(only A) = n(A) – n($A\cap B$) – n($A\cap C$) + n($A\cap B\cap C$)
Where A, B and C are just like the above three subjects.
So, let’s find only mathematics first.
N(only M) = n(M) – n($M\cap P$) – n($M\cap C$) + n($M\cap P\cap C$)
Now, place all the values given in the data.
N(only M) = 100 – 30 – 28 + 18
Solve now:
N(only M) = 60
Similarly, we will find only Physics.
N(only P) = n(P) – n($M\cap P$) – n($P\cap C$) + n($M\cap P\cap C$)
Now, place all the values given in the data.
N(only P) = 70 – 30 – 23 + 18
Solve now:
N(only P) = 55
Now, we will calculate for chemistry also.
N(only C) = n(C) – n($M\cap C$) – n($P\cap C$) + n($M\cap P\cap C$)
Now, place all the values given in the data.
N(only C) = 46 – 28 – 23 + 18
Solve now:
N(only C) = 33
Number of students for mathematics alone: 60
Number of students for Physics alone: 55
Number of students for chemistry alone: 33
To find the number of students who have not offered any of these subjects, first we have to find the union of the three subjects. For that formula will be:
N($A\cup B\cup C$) = n(A) + n(B) + n(C) - n($A\cap B$) - n($B\cap C$) - n($A\cap C$) + n($A\cap B\cap C$)
For three subjects, the formula will be:
N($M\cup P\cup C$) = n(M) + n(P) + n(C) - n($M\cap P$) - n($M\cap C$) - n($P\cap C$) + n($M\cap P\cap C$)
Place all the values in the above formula from the data set given:
N($M\cup P\cup C$) = 100 + 70 + 46 – 30 – 28 – 23 + 18
On solving we get:
N($M\cup P\cup C$) = 153
Now, for obtaining the number of students who are not offering any of the subjects, it will be represented as: not(M, P, C).
not(M, P, C) = n(U) – n($M\cup P\cup C$)
U stands for universal set and in universal set, the total of students in class is 175.
not(M, P, C) = 175 – 153 = 22
So, 22 students are not offering any of the three subjects.

Note: Students usually make mistakes when they think that the number of students particularly given for each subject are for only that particular subject. Like for mathematics it is given n(M) = 100 so it doesn’t mean that it is given for n(only M), rather it includes n(only M) and also the intersection with other subjects. It does not belong purely for that particular subject. Do remember where to use union and intersection symbols.