Question

A circus tent is cylindrical upto a height of 3m and conical above. If the diameter of the base is \[105m\] and the slant height of the conical part is \[53m\], find the total canvas used in making the tent.

Answer 1

Hint: In this question, we have to give a circus tent cylindrical up to and conical above. It means the diameter of the base of the cylinder is the same as the diameter of the base of the cone. In which we find the canvas used in making the tent. So firstly we will find the curved surface area of the cylinder and then find the curved surface area of the cone. So the required canvas is the sum area of the cone. So the required canvas is the sum of curved surface area of cylinder and curved surface area of cone.

Complete step-by-step answer:

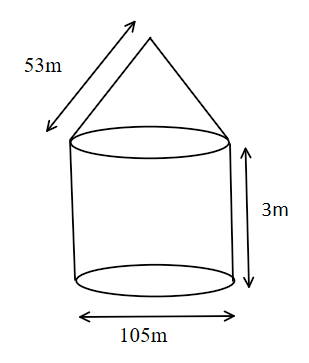
Given, the diameter of base of cylinder\[ = 105m\]
We know that the radius of the base of the cylinder is half of the diameter.
That is, radius \[ = \dfrac{{105}}{2}m\]
Height of the cylinder \[ = 3m\]
Curved surface area of cylinder \[ = 2\pi rh\]
Using \[\pi = \dfrac{{22}}{7}\]
So, after put the value, we get
Curved surface area of cylinder\[ = 2 \times \dfrac{{22}}{7} \times \dfrac{{105}}{2} \times 3\]
After solving, We get \[ = 22 \times 15 \times 3\]
\[ = 990{m^2}\]
Step2: Given, Diameter of base of cone \[ = 105m\]
Radius of base of cone \[ = \dfrac{{105}}{2}m\]
Slant height \[ = 53m\]
Curved surface area of cone \[ = 17 \times radius\; \times slant{\text{ }}height\]
\[ = \dfrac{{22}}{7} \times \dfrac{{105}}{2} \times 55\]
After solving, we get curved surface area of cone \[ = 11 \times 15 \times 55\]
\[ = 9075{m^2}\]
Total canvas use in making a tent is the sum of curved surface area of cylinder and curved surface area of cone.
That is, total canvas used in making tent \[ = C.S.A{\text{ }}of{\text{ }}cylinder + {\text{ }}C.S.A{\text{ }}of{\text{ }}cone\;\;\]
\[ = 990{m^2} + 9075{m^2}\]
After solving, we get \[ = 10065{m^2}\]
So, the required canvas for making a tent is \[10065\] meter square.

Note: If we take a number of circular sheets of paper and stack them up as we stacked up rectangular sheets. Here if the stack is kept vertically up, we get a right circular cylinder, since it has been kept at right angles to the base and the base is circular.