Question

A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.

Answer 1

Hint:
 In this question we will use trigonometric ratios. Trigonometry is a branch of mathematics which deals with the measurement of sides and angles of a triangle and the problems based on them. Trigonometry helps us to find angles and distances, and is used a lot in science, engineering, and many more.
There are many trigonometry formulas and trigonometric identities, which are used to solve complex equations in geometry.
The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle. They are defined by parameters namely hypotenuse, base and perpendicular.
In ∆ABC
$\sin \theta = \dfrac{{Perpendicular}}{{Base}}$

$\sin \theta = \dfrac{{AB}}{{AC}}$
And the value of \[\sin 30^\circ \] is $\dfrac{1}{2}$

Complete step by step solution:
Let the height of pole be AB = h
It is given that,
Length of the rope = 20m

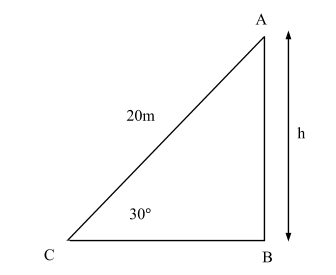
We assume that rope is tied at ground level at point C
∴AC = 20m
Angle made by rope with the ground level = 30°
\[\begin{gathered}
  \therefore \angle ACB = 30^\circ \\
  {\text{and }}\angle ABC = 90^\circ \\
\end{gathered} \]
We know that
$\sin \theta = \dfrac{{Perpendicular}}{{Base}}$
$\sin 30^\circ = \dfrac{{AB}}{{AC}}$
$\begin{gathered}
  \dfrac{1}{2} = \dfrac{h}{{20}} \\
  h = \dfrac{1}{2} \times 20 \\
  h = 10m \\
\end{gathered} $
∴ Height of the pole = h = 10m

Note:
There are 6 trigonometric ratios, Sine (sin), Cosine (cos), Tangent (tan), Cosecant (cosec), Secant (sec), Cotangent (cot)
$\sin \theta = \dfrac{{Perpendicular}}{{Base}}$

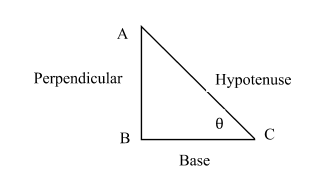
$\begin{gathered}
  \cos \theta = \dfrac{{Base}}{{Hypotenuse}} \\
  \tan \theta = \dfrac{{Perpendicular}}{{Base}} \\
  \cos ec\theta = \dfrac{{Hypotenuse}}{{Perpendicular}} \\
  \sec \theta = \dfrac{{Hypotenuse}}{{Base}} \\
  \cot \theta = \dfrac{{Base}}{{Perpendicular}} \\
\end{gathered} $
Some of the basic applications of trigonometry are:
Measuring the heights of towers or big mountains.
Determining the distance of the shore from the sea.
Finding the distance between two bodies.
Determining the power output of solar cell panels at different inclinations.