Question

A circular road of radius $r$ is banked for a speed $\nu = 40 kmph$. A car of mass $m$ attempts to go on the circular road. The friction coefficient between the tyre and the road is negligible.
A) The car cannot make a turn without skidding
B) If the car turns less than speed $40 $ km/hr, it will slip down
C) If the car turns at the correct speed of $40 $ km/hr, the force by the road on the car is equal to $\dfrac{{m{\nu ^2}}}{r}$
D) If the car turns at the correct speed of $40 $ km/hr, the force by the road on the car is greater than $mg$ as well as greater than $\dfrac{{m{\nu ^2}}}{r}$

Answer 1

Hint: The road of radius $r$ can be thought of having a small bending angle $\theta $. The friction coefficients said to be negligible. So, to solve the problem you need to basically identify the forces acting on the body and balance out appropriately. You can now break the normal force that is the force exerted on the body by the road, in two components. One will compensate for the gravitational attraction and another will supply the required centripetal force to keep the car in rotational motion.

Complete step by step answer:
Given:
The mass of the car is $m$.
The radius of the circular road is $r$.
The car is banked for a speed of $\nu = 40 $ km/hr.
The friction co-efficient $\mu = 0$.

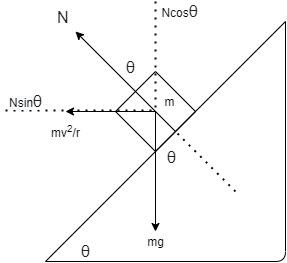
Step 1:
Break the normal reaction exerted on the car by the road in two components.
From the figure it is evident that the component $N\cos \theta $ balances the force due to gravity that is $mg$.
$N\cos \theta = mg$
Similarly, as there is no friction, hence, you can see that the component $N\sin \theta $ actually supplies the required centripetal force for the car to be on the road in uniform motion.
Hence,
$N\sin \theta = \dfrac{{m{\nu ^2}}}{r}$
Step 2:
Now divide the eq (2) by eq (1) to get
$
  \dfrac{{N\sin \theta }}{{N\cos \theta }} = \dfrac{{\dfrac{{m{\nu ^2}}}{r}}}{{mg}} \\
   \Rightarrow \tan \theta = \dfrac{{{\nu ^2}}}{{rg}} \\
 $
So, from this you can get the velocity $\nu $ for which the car on the circular road, can turn with horizontal and vertical equilibrium, that is the car will not slide.
$\nu = \sqrt {rg\tan \theta } $
So, it is clear that (A) cannot be a correct option.
Step 3:
Now as the road banked for the speed $\nu = 40$ km/hr.
So, if the speed of the car ${\nu _{car}}$ is lesser than $\nu $, then the component $N\sin \theta $ shall be greater than the $\dfrac{{m{\nu _{car}}^2}}{r}$, hence, you can see that the car will slip down.
So, the option (B) is a correct option.
Step 4:
Now, if the speed of the car ${\nu _{car}}$ is exactly same as $\nu = 40$ km/hr. Then eq (1) and (2) are satisfied.
Now from eq (2) express the normal reaction
$
  N\sin \theta = \dfrac{{m{\nu ^2}}}{r} \\
   \Rightarrow N = \dfrac{{m{\nu ^2}}}{{r\sin \theta }} \\
 $
$\therefore $ The option (C) turns out to be incorrect.
Step 5:
You can easily understand for practical reasons the banking angle $\theta $ should be lesser than $\dfrac{\pi }{2}$.
So, check the eq (4) for $\theta < \dfrac{\pi }{2}$ .
$
  \because \theta < \dfrac{\pi }{2},\therefore \sin \theta < 1 \\
   \Rightarrow \dfrac{1}{{\sin \theta }} > 1 \\
  \therefore N = \dfrac{{m{\nu ^2}}}{{r\sin \theta }} > \dfrac{{m{\nu ^2}}}{r} \\
 $
So, you can see the force by the road on the car that is the normal reaction $N$ is greater than $\dfrac{{m{\nu ^2}}}{r}$.
Step 6:
Express the normal reaction $N$ from the eq (1).
$
  N\cos \theta = mg \\
   \Rightarrow N = \dfrac{{mg}}{{\cos \theta }} \\
$
For the road to be circular with a banking angle $\theta $, we should have $0 < \theta < \dfrac{\pi }{2}$.
So, in the region, you have $\cos \theta < 1$ and similarly $\dfrac{1}{{\cos \theta }} > 1$.
From, eq (5)
$\therefore N = \dfrac{{mg}}{{\cos \theta }} > mg$
So, you can see the force by the road on the car that is the normal reaction $N$ is greater than greater than $mg$.

Therefore, the correct options are :
(B) If the car turns less than a speed $40$ km/hr, it will slip down.
(D) If the car turns at the correct speed of $40$ km/hr, the force by the road on the car is greater than $mg$ as well as greater than $\dfrac{{m{\nu ^2}}}{r}$.

Note:
The main problem that you may face is to understand the normal reaction $N$. Clearly, this is the force exerted on the body from the plane where it resides and that too normally independent of the horizontal or vertical direction. Similarly, gravitation being a central force acts vertically downwards from the center of the mass of the car.
So, basically not the normal force itself, but, the vertical component of the normal force balances the force due to gravity.
Similarly, the horizontal component supplies the required centripetal force to keep the car on the circular motion and thus also keeping it on the circular path.
So only at the banking speed, all the forces are in equilibrium, both horizontally and vertically.