Question

A circular race track has a radius of 500m and is banked to $10^\circ $ . If the coefficient of friction between the tyres of a vehicle and the road surface is $0 \cdot 25$ , compute (a) maximum speed to avoid slipping, (b) the optimum speed to avoid wear and tear of the tyres. (Take $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ ).

Answer 1

Hint: The forces acting on the vehicle moving along the circular track are its weight, the frictional force, the normal reaction force and the centrifugal force. Sketching a free body diagram of the vehicle moving along the banked circular track will help us to take into account the components of these forces to derive an expression for the maximum velocity of the vehicle so that it does not slip.

Formula used:
-The maximum velocity to avoid slipping is given by, ${v_{\max }} = \sqrt {\dfrac{{rg\left( {\tan \theta + \mu } \right)}}{{1 - \mu \tan \theta }}} $ where $r$ is the radius of the circular path, $g$ is the acceleration due to gravity, $\theta $ is the angle at which the path is banked and $\mu $ is the coefficient of friction.
-The optimum velocity to avoid wear and tear is given by, ${v_{optimum}} = \sqrt {rg\tan \theta } $ where $r$ is the radius of the circular path, $g$ is the acceleration due to gravity and $\theta $ is the angle at which the path is banked.

Complete step by step solution:
Step 1: Sketch a free body diagram to resolve the components of the various forces in action.
Let $m$ be the mass and $v$ be the velocity of the vehicle moving along the circular track.

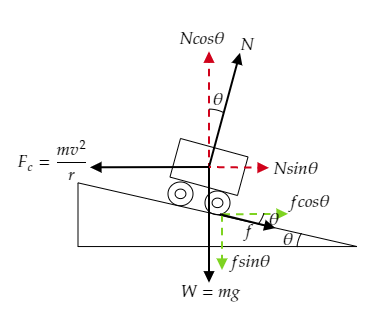
In the above figure, the frictional force $f$ is resolved into its components $f\cos \theta $ and $f\sin \theta $. The normal reaction force $N$ is also resolved into its components $N\cos \theta $ and $N\sin \theta $. The weight of the vehicle $W = mg$ is acting downwards and the centrifugal force ${F_c} = \dfrac{{m{v^2}}}{r}$ is acting away from the centre of the track.
The track is given to be banked to an angle $\theta = 10^\circ $ .
The radius of the race track is given to be $r = 500{\text{m}}$ .
The coefficient of friction between the tyres of the vehicle and the road is given to be $\mu = 0 \cdot 25$.
Let $m$ be the mass and $v$ be the velocity of the vehicle moving along the circular track.
Step 2: Apply the force balance equation to derive an expression for maximum velocity without slipping.
For the force balance equation along the vertical direction, the total forces acting in the upward direction must be equal to the total forces acting in the downward direction.
i.e., ${F_{upward}} = {F_{downward}}$
$ \Rightarrow N\cos \theta = mg + f\sin \theta $
$ \Rightarrow mg = N\cos \theta - if\sin \theta $ --------- (1)
Similarly, for the force balance equation along the horizontal direction, we have $\dfrac{{m{v^2}}}{r} = N\sin \theta + f\cos \theta $ --------- (2)
Now dividing equation (2) by (1) we get, $\dfrac{{\left( {\dfrac{{m{v^2}}}{r}} \right)}}{{mg}} = \dfrac{{N\sin \theta + f\cos \theta }}{{N\cos \theta - if\sin \theta }}$ ------- (3)
The frictional force is expressed as $f = \mu N$ .
Then equation (3) becomes $\dfrac{{{v^2}}}{{rg}} = \dfrac{{N\sin \theta + \mu N\cos \theta }}{{N\cos \theta - \mu N\sin \theta }}$
Or, on simplifying this becomes $\dfrac{{{v^2}}}{{rg}} = \dfrac{{\sin \theta + \mu \cos \theta }}{{\cos \theta - \mu \sin \theta }}$
Dividing the numerator and denominator of the above expression by $\cos \theta $ we get, $\dfrac{{{v^2}}}{{rg}} = \dfrac{{\tan \theta + \mu }}{{1 - \mu \tan \theta }}$
$ \Rightarrow v = \sqrt {\dfrac{{rg\left( {\tan \theta + \mu } \right)}}{{1 - \mu \tan \theta }}} $ --------- (4)
Equation (4) is the required expression for the maximum velocity of the vehicle.
Step 3: Substitute appropriate values in equation (4) to obtain the maximum velocity without slipping.
The maximum velocity of the car to avoid slipping is given by equation (4) as ${v_{\max }} = \sqrt {\dfrac{{rg\left( {\tan \theta + \mu } \right)}}{{1 - \mu \tan \theta }}} $
Substituting for $\theta = 10^\circ $ , $r = 500{\text{m}}$ , $\mu = 0 \cdot 25$ and $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ in the above expression we get, ${v_{\max }} = \sqrt {\dfrac{{500 \times 9 \cdot 8 \times \left( {\tan 10^\circ + 0 \cdot 25} \right)}}{{1 - \left( {0 \cdot 25 \times \tan 10^\circ } \right)}}} = 46 \cdot 75{\text{m}}{{\text{s}}^{ - 1}}$
$\therefore $ the maximum velocity to avoid slipping is obtained to be ${v_{\max }} = 46 \cdot 75{\text{m}}{{\text{s}}^{ - 1}}$ .
Step 4: Substitute $\mu = 0$ in equation (4) to obtain the expression of optimum velocity.
When $\mu = 0$ , the optimum velocity of the vehicle becomes ${v_{optimum}} = \sqrt {rg\tan \theta } $ ------ (5)
Substituting for $\theta = 10^\circ $ , $r = 500{\text{m}}$ and $g = 9 \cdot 8{\text{m}}{{\text{s}}^{ - 2}}$ in equation (5) we get, ${v_{optimum}} = \sqrt {500 \times 9 \cdot 8 \times \tan 10^\circ } = 29 \cdot 39{\text{m}}{{\text{s}}^{ - 1}}$
$\therefore $ the optimum speed to avoid wear and tear is obtained to be ${v_{optimum}} = 29 \cdot 39{\text{m}}{{\text{s}}^{ - 1}}$ .

Note: For the vehicle to avoid slipping, it should get some kind of grip on the road. This grip is provided by the friction present between the tyres of the vehicle and the road. So while obtaining the maximum velocity to avoid slipping we take into account the frictional force. However, the tyres of the vehicle will wear and tear due to the friction present between the tyres and the road. So we discard friction and take $\mu = 0$ while expressing the optimum velocity of the vehicle to avoid wear and tear.