Question

A circular hole is filled with concrete to make a footing for a load-bearing pier. The hole measures 17 inches across and requires 1.6 bags of concrete in order to fill it to ground level. What is the depth of the hole? Round your answer to the nearest inch. (One bag of concrete, when mixed with the appropriate amount of water, makes 1800in.3 of material).
A. 17 in.
B. 10 in.
C. 19 in.
D. 13 in.

Answer 1

Hint: 1. Diameter of a circle = 2 x radius of the circle
2. Volume of a cylinder whose radius is ‘r’ and has a height ‘h’ can be found out by using the formulae = $ \pi {r^2}h $

Complete step-by-step answer:
The above situation can be explained by this diagram:

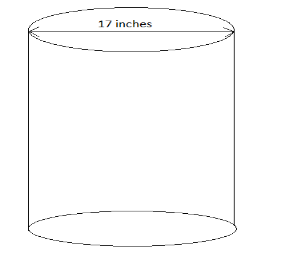
We are provided with the data that:
1. Diameter of the circular hole = 17 inches
 Radius of the circular hole = $ \dfrac{{Diameter}}{2} $
 $ \dfrac{{17}}{2} $ inches
2. Volume of cylindrical hole = $ \pi {r^2}h $ ......(1)
And, the total volume of cylindrical hole will be occupied by 1.6 bags of concrete ......(2)
Therefore, from Eqn (1) and (2)
Volume of cylindrical hole = volume occupied by 1.6 bags of concrete
  $ \pi {r^2}h $ = 1.6 x (Volume occupied by 1 bag of concrete)
 $ \dfrac{{22}}{7} \times {\left( {\dfrac{{17}}{2}} \right)^2} \times h = 1.6 \times 1800 $
Dividing both sides by $ \dfrac{{22}}{7} $ and $ {\left( {\dfrac{{17}}{2}} \right)^2} $ , we get
 $ h = \dfrac{{1.6 \times 1800}}{{\dfrac{{22}}{7} \times {{\left( {\dfrac{{17}}{2}} \right)}^2}}} $
Simplifying the given equation, we get
 $ h = \dfrac{{1.6 \times 1800 \times 7 \times 2 \times 2}}{{22 \times 17 \times 17}} $
Simplifying the numerator and denominator, we get
 $ \begin{gathered}
  h = \dfrac{{80640}}{{6358}} \\
  h = 12.6 \\
  h \approx 13 \\
\end{gathered} $
The depth of the hole will be approximately equal to 13 inches.

Note: It is essential to note that 1 bag of concrete contributes to 1800 inch³ of concrete for the cylindrical pipe. So if we want to find out the volume occupied by 1.6 bags of concrete then it must be multiplied with 1800 inch³ first.