Question

A circular grass lawn of 35m in radius has a path 7m running around it on the outside. The area of the path is?
A) $1,496{m^2}$
B) $1,450{m^2}$
C) $1,576{m^2}$
D) $1,694{m^2}$

Answer 1

Hint:
We can find the radius of the park including the path by adding the radius of the park and the width of the path. Then we can find the area of the park including the path using the new radius. Then we can find the area of the park without the path using the given radius of the park. Then we can find the difference in their area to find the area of the path.

Complete step by step solution:

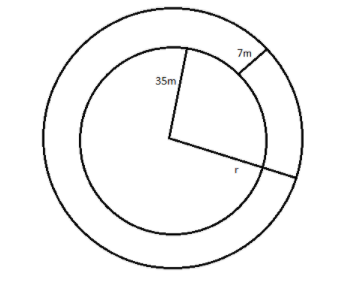
We are given that the radius of the park is 35m and the width of the path is 7 m.
Then, ${r_1} = 35m$ and $d = 7m$
Let the radius of the park including the path be ${r_2}$ .
Then we can write,
 $ \Rightarrow {r_2} = {r_1} + d$
On substituting the values, we get,
 $ \Rightarrow {r_2} = 35 + 7$
 $ \Rightarrow {r_2} = 42$
Now we can find the area of the park including the path.
 ${A_2} = \pi {r_2}^2$
On substituting the values, we get,
 $ \Rightarrow {A_2} = \dfrac{{22}}{7} \times {\left( {42} \right)^2}$
On cancelling the common factors, we get,
 $ \Rightarrow {A_2} = 22 \times 42 \times 6$
On multiplication, we get,
 $ \Rightarrow {A_2} = 5544$
Now we can find the area of the park excluding the path.
 ${A_1} = \pi {r_1}^2$
On substituting the values, we get,
 $ \Rightarrow {A_1} = \dfrac{{22}}{7} \times {\left( {35} \right)^2}$
On cancelling the common factors, we get,
 $ \Rightarrow {A_1} = 22 \times 35 \times 5$
On multiplication, we get,
 $ \Rightarrow {A_1} = 3850$
Now the area of the path is given by the difference between these 2 areas.
So, the required area is,
 $ \Rightarrow A = {A_2} - {A_1}$
On substituting the values, we get,
 $ \Rightarrow A = 5544 - 3850$
 $ \Rightarrow A = 1694$
Therefore, the area of the path is $1,694{m^2}$ .

So, the correct answer is option D.

Note:
We must draw a diagram to understand the question. We must add the width of the path with given radius and not subtract from it. We must not take the square of the difference in the radii for finding the area. We must use the fractional value of $\pi $ as the radii are multiples of 7.
Alternate method to find the area of the path is,
 $ \Rightarrow A = {A_2} - {A_1}$
 $ \Rightarrow A = \pi {r_2}^2 - \pi {r_1}^2$
On taking \[\pi \] common we get,
 \[ \Rightarrow A = \pi \left( {{r_2}^2 - {r_1}^2} \right)\]
On applying the identity, we get,
 \[ \Rightarrow A = \pi \left( {{r_2} - {r_1}} \right)\left( {{r_2} + {r_1}} \right)\]
On substituting the values, we get,
 \[ \Rightarrow A = \dfrac{{22}}{7}\left( {42 - 35} \right)\left( {42 + 35} \right)\]
On simplification, we get,
 \[ \Rightarrow A = \dfrac{{22}}{7} \times 7 \times 77\]
On cancelling 7 we get,
 \[ \Rightarrow A = 22 \times 77\]
On multiplication we get,
 \[ \Rightarrow A = 1694\]
Therefore, the area of the path is $1,694{m^2}$.