Question

A circular field has a perimeter of 650m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square plot.

Answer 1

Hint: Start by drawing the diagram. Once you have drawn the diagram use the property that the diagonals of the square are equal to the diameter of the circle in which it is inscribed. Also, use the formula that the area of a square is equal to half of the square of its diagonals.
Complete step-by-step answer:
Let us start by drawing the figure of the situation given in the question for better visualisation.

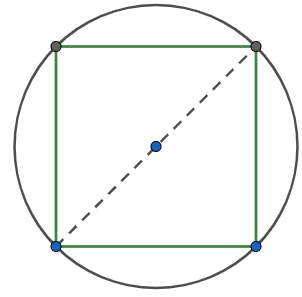
Now from the figure, we can easily figure out that the centre of the circle and the square are the same and the diameter of the circle is the diagonal of the square. So, to start with the question we let the radius of the circle to be r.
It is given in the question that the perimeter of the circle is 650 m.
$\therefore \text{Perimeter of the circle=2}\pi \text{r}$
$\Rightarrow \text{650=2}\pi \text{r}$
$\Rightarrow r=\dfrac{325}{\pi }\text{ cm}$
Now, the diameter of the circle is twice its radius, so the length of the diameter is $2r=\dfrac{650}{\pi }\text{ cm}$ . Therefore, the diagonal of the square is also equal to $2r=\dfrac{650}{\pi }\text{ cm}$ .
Also, we know that the area of a square is equal to half of the square of its diagonals.
$\therefore \text{ Area of the square=}\dfrac{1}{2}{{\left( \text{diagonal}\right)}^{2}}$
$\Rightarrow \text{Area of the square=}\dfrac{1}{2}{{\left( \dfrac{650}{\pi } \right)}^{2}}$
Now, if we put the value of $\pi $ to be 3.14, we get
$\text{Area of the square=}\dfrac{1}{2}{{\left( 207 \right)}^{2}}=21424.5\text{ c}{{\text{m}}^{2}}$
Therefore, the answer to the above question is 21424.5 sq cm.

Note: In such questions, be careful about the calculation part and the value of $\pi $ you put, as general mistakes are made in calculation parts. Also, you need to learn all the formulas related to perimeter and areas of different geometrical figures like circle, square, rectangle etc. We can find the length of the side of the square first using diagonal and we can find the area.