
A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs touch. The centre of mass of the new disc is at a distance $\alpha R$ from the centre of the bigger disk. The value of $\alpha $ is:
A. $\dfrac{1}{2}$
B. $\dfrac{1}{3}$
C. $\dfrac{1}{4}$
D. $\dfrac{1}{6}$
Answer
584.1k+ views
Hint: Centre of mass of a disc is positioned at the centre of the disc. So, the effective centre of mass of the removed portion and the remaining portion should be at the centre of the bigger disc. Calculate the mass of each segment and calculate the centre of mass of the system after putting two at the original positions. The calculated value should be at the centre of the original disc.
Formula Used:
The position vector of effective centre of mass due to two objects is given by,
${{\vec{x}}_{cm}}=\dfrac{{{M}_{1}}{{{\vec{x}}}_{1}}+{{M}_{2}}{{{\vec{x}}}_{2}}}{{{M}_{1}}+{{M}_{2}}}$.....................(1)
Where,
${{M}_{1}}$ is the mass of the first object
${{\vec{x}}_{1}}$ is the position vector of the first object
${{M}_{2}}$ is the mass of the second object
${{\vec{x}}_{2}}$ is the position vector of the second object
Complete step by step answer:
At first, let us look at the following diagram:
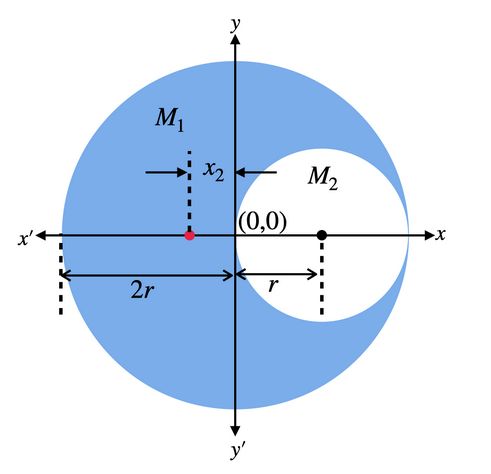
This diagram shows the positions of the centre of mass of each object. Let’s assume that the centre of mass of the remaining part is the red dot, which is at a distance of
${{\vec{x}}_{2}}$, from the origin.
We are assuming that the density of the disc is uniform.
Let’s assume that the mass of the remaining disc is,
${{M}_{2}}$
And the mass of the cutout portion is,
${{M}_{1}}$
Mass of the disc depends on the area. So, we can write,
$\dfrac{{{M}_{1}}}{{{M}_{1}}+{{M}_{2}}}=\dfrac{\pi {{R}^{2}}}{4\pi {{R}^{2}}}$
$\Rightarrow 4{{M}_{1}}={{M}_{1}}+{{M}_{2}}$
$\Rightarrow 3{{M}_{1}}={{M}_{2}}$
Hence,
$3{{M}_{1}}={{M}_{2}}$
The centre of mass before cut out was at the centre.
The centre of mass of the cut-out portion was at, (R,0)
We are using the concept that, if we put the cutout section, and remaining disc at the original position, it will give back the original disc.
So, the effective centre of mass will be at the origin.
Hence we can write,
$0=\dfrac{{{M}_{1}}(R)+{{M}_{2}}({{x}_{2}})}{{{M}_{1}}+{{M}_{2}}}$
$\Rightarrow {{M}_{1}}(R)+{{M}_{2}}({{x}_{2}})=0$
$\Rightarrow {{x}_{2}}=-\dfrac{{{M}_{1}}}{{{M}_{2}}}R$
Hence,
$\Rightarrow {{x}_{2}}=-\dfrac{1}{3}R$
So, the distance of the centre of the big disc after the cut out is, $\dfrac{R}{3}$ on the left.
Hence,
$\alpha =\dfrac{1}{3}$
The correct option is (B).
Note: We have not considered the y-direction because there is no change of centre of mass in the y-direction. Otherwise, you can use vector equations. You can reorient the axis to have the least calculation.
You should draw the diagram before proceeding with the solution. This will help in reducing some unnecessary mistakes.
Formula Used:
The position vector of effective centre of mass due to two objects is given by,
${{\vec{x}}_{cm}}=\dfrac{{{M}_{1}}{{{\vec{x}}}_{1}}+{{M}_{2}}{{{\vec{x}}}_{2}}}{{{M}_{1}}+{{M}_{2}}}$.....................(1)
Where,
${{M}_{1}}$ is the mass of the first object
${{\vec{x}}_{1}}$ is the position vector of the first object
${{M}_{2}}$ is the mass of the second object
${{\vec{x}}_{2}}$ is the position vector of the second object
Complete step by step answer:
At first, let us look at the following diagram:

This diagram shows the positions of the centre of mass of each object. Let’s assume that the centre of mass of the remaining part is the red dot, which is at a distance of
${{\vec{x}}_{2}}$, from the origin.
We are assuming that the density of the disc is uniform.
Let’s assume that the mass of the remaining disc is,
${{M}_{2}}$
And the mass of the cutout portion is,
${{M}_{1}}$
Mass of the disc depends on the area. So, we can write,
$\dfrac{{{M}_{1}}}{{{M}_{1}}+{{M}_{2}}}=\dfrac{\pi {{R}^{2}}}{4\pi {{R}^{2}}}$
$\Rightarrow 4{{M}_{1}}={{M}_{1}}+{{M}_{2}}$
$\Rightarrow 3{{M}_{1}}={{M}_{2}}$
Hence,
$3{{M}_{1}}={{M}_{2}}$
The centre of mass before cut out was at the centre.
The centre of mass of the cut-out portion was at, (R,0)
We are using the concept that, if we put the cutout section, and remaining disc at the original position, it will give back the original disc.
So, the effective centre of mass will be at the origin.
Hence we can write,
$0=\dfrac{{{M}_{1}}(R)+{{M}_{2}}({{x}_{2}})}{{{M}_{1}}+{{M}_{2}}}$
$\Rightarrow {{M}_{1}}(R)+{{M}_{2}}({{x}_{2}})=0$
$\Rightarrow {{x}_{2}}=-\dfrac{{{M}_{1}}}{{{M}_{2}}}R$
Hence,
$\Rightarrow {{x}_{2}}=-\dfrac{1}{3}R$
So, the distance of the centre of the big disc after the cut out is, $\dfrac{R}{3}$ on the left.
Hence,
$\alpha =\dfrac{1}{3}$
The correct option is (B).
Note: We have not considered the y-direction because there is no change of centre of mass in the y-direction. Otherwise, you can use vector equations. You can reorient the axis to have the least calculation.
You should draw the diagram before proceeding with the solution. This will help in reducing some unnecessary mistakes.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




