Question

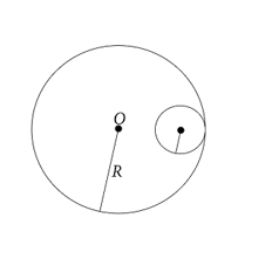
A circular disc of radius $\dfrac{R}{3}$ is cut from a circular disc of radius $R$ and mass $9M$ as shown. Then moment of inertia of remaining disc about O which is perpendicular to the plane of the disc is:

\[\begin{align}
  & A.4M{{R}^{2}} \\
 & B.9M{{R}^{2}} \\
 & C.\dfrac{37}{9}M{{R}^{2}} \\
 & D.\dfrac{40}{9}M{{R}^{2}} \\
\end{align}\]

Answer 1

Hint: Moment of inertia is a calculation of the resistance of a body to the angular acceleration about a certain axis that is equivalent to the sum of the products of each element of mass in the body and the square of the element's distance from the axis.

Complete step by step answer:

The moment of inertia is defined as a physical quantity which explains how easily a body can be rotated about a certain axis. It is given as the rotational analogue of mass, which explains the resistance of an object to the translational motion.
As we all know, the moment of inertia of a circular disc with radius $R$ and mass $9M$ is written as,
${{I}_{total}}=\dfrac{9M{{R}^{2}}}{2}$
The mass of the cut out portion with a radius of $\dfrac{R}{3}$ is given as,
$m=9M\dfrac{\pi {{\left( \dfrac{R}{3} \right)}^{2}}}{\pi {{R}^{2}}}=M$
Therefore now we know that, $M$ is the mass of the cut out portion of the disc.
Therefore its moment of inertia of the cut out portion about the centre O is,
$\begin{align}
  & {{I}_{cutout}}={{I}_{0}}+m{{\left( \dfrac{2R}{3} \right)}^{2}}=\dfrac{m{{\left( \dfrac{R}{3} \right)}^{2}}}{2}+m{{\left( \dfrac{2R}{3} \right)}^{2}} \\
 & =\dfrac{M{{R}^{2}}}{2} \\
\end{align}$
Therefore the moment of inertia of the remaining portion of the circular disc will be,
${{I}_{remaining}}=9M\dfrac{{{R}^{2}}}{2}-M\dfrac{{{R}^{2}}}{2}=4M{{R}^{2}}$

So, the correct answer is “Option A”.

Note:
The moment of inertia of a body is directly proportional to the mass of the object and it increases as the mass is being moved further from the axis of rotation. The concept that moment of inertia depends on the mass distribution means that the similar body can have different moments of inertia which is depending on which axis of rotation we are taking. As per the conservation of angular momentum, if the moment of inertia decreases. The angular velocity will decrease to keep angular momentum a constant.