Question

A circular coin is placed on a table. four equal larger coins are placed around the first coin, so that each touches the coin and also two of the larger coins if the radius of the first coin is r and the of the others is 5 cm, find r

Answer 1

Hint: To handle such type of questions we will use the underneath steps
Here we will use Pythagoras theorem. When two circle touches each other line joining the center is perpendicular to the common tangent
Given: 5 circles are there. 4 are larger and one is small.

Complete step-by-step answer:
When we are solving this type of question, we need to follow the steps provided in the hint part above.

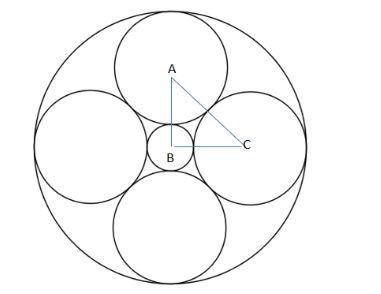
Above figure shows the orientation of the circles.
Our solution will be based on that
AC = 5+5 =10
AB = 5+r
BC =5+r
By Pythagoras theorem
\[\begin{array}{l}
A{C^2} = A{B^2} + B{C^2}\\
{10^2} = {(5 + r)^2} + {(5 + r)^2}\\
{10^2} = 2{(5 + r)^2}\\
5\sqrt 2 = 5 + r\\
r = 5(\sqrt 2 - 1)\\

\end{array}\]
Hence radius of inner circle is \[5(\sqrt 2 - 1)\]
Hence after following the each and every step given in the hint part we obtained our final answer.

Additional Information:
Here we can clearly see that in this solution we did not use any complicated process because we followed basic and simple things in the right order as per given in the above hint section.

Note: In this sort of examples, we need to face the various things and some of them are referred to here which will be really helpful to fathom the main concept of problem:
We need to use right formula to avoid unnecessary things which are sometime time consuming: