Question

A circle with largest area is cut from a rectangular card-board with dimensions 55 cm $\times$ 42 cm. then the ratio between the area of the circle cut and the area of the remaining card-board be
(a) 3:2
(b) 6:4
(c) 13:2
(d) 3:12

Answer 1

Hint: First we need to find the area of the given rectangular card-board $(l\times b)$ . Then we need the area of the largest circle $(\pi {{r}^{2}})$ that can be cut from the given card-board. Lastly, to get the area of the remaining card-board, we will subtract the area of the largest circle from the rectangular card-board. then, we will find the required ratio.

Complete step by step solution:
Let us consider a rectangular card-board ABCD having length 55 cm and breadth 42 cm. Then we will draw the largest circle inside the rectangular card-board.

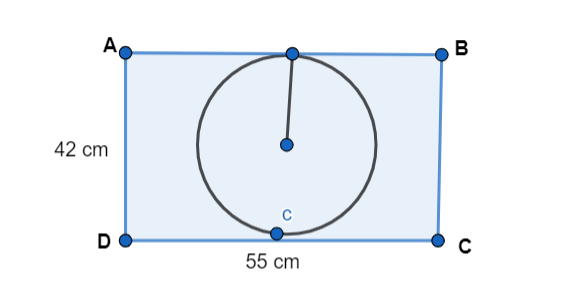
We are given a rectangular piece of card-board whose dimensions are
length (l) = 55 cm
Breadth (b) = 42cm
Now, a circle with the largest area is cut from the given rectangular card-board.
Therefore, diameter of the largest circle(d)=42 cm
Radius of the largest circle (r) = $\dfrac{d}{2}$
Substituting the value of diameter, we have radius(r) as
$\begin{align}
  & =\dfrac{42}{2} \\
 & =21cm \\
\end{align}$
$\Rightarrow $ radius (r)= 21 cm
Now, the area of rectangular card-board
 $\begin{align}
  & =l\times b \\
 & =\left( 55\times 42 \right) \\
 & =2310c{{m}^{2}} \\
\end{align}$
Also, the area of the largest circle
$\begin{align}
  & =\pi {{r}^{2}} \\
 & =\dfrac{22}{7}\times 21\times 21 \\
 & =22\times 3\times 21 \\
 & =1386c{{m}^{2}} \\
\end{align}$
Again, the area of the remaining piece card-board= (area of the rectangular card-board)-(area of the largest circle)
$\begin{align}
  & =(2310-1386) \\
 & =924c{{m}^{2}} \\
\end{align}$
Therefore, the ratio of the area of largest circle to the area of remaining card-board
$\begin{align}
  & =1386:924 \\
 & =3:2 \\
\end{align}$
But if we look carefully on the option given in (b) it is also correct.
Hence option (a) and option (b) both are correct.

Note: Many numbers of circles can be made from a rectangle. But in the given question demand the largest circle of that rectangle. So, always remember that the diameter of the largest circle is equal to the breadth of the rectangle. In most of the questions, if the figure is not given then we need to draw the figure by ourselves. Here in the options we can see that option (b) is also correct. So we conclude that the question may have multiple correct options.