Question

A circle with centre at $(15, - 3)$ is tangent to $y = \dfrac{{{x^2}}}{3}$ at a point in the first quadrant. The radius of the circle is equal to
$\begin{gathered}
  A - 5\sqrt 6 \\
  B - 8\sqrt 3 \\
  C - 9\sqrt 2 \\
  D - 6\sqrt 5 \\
\end{gathered} $

Answer 1

Hint: This sum is from the chapter Curves. Students have to first draw whatever curves are given and then use a structured approach to solve. In this sum after drawing the curve students will get to know that they have to first find the slopes of the tangent and the Line from centre to the tangent. Then with the trial and error method find the coordinates of the point of intersection of tangent to the curve. Last step involves using distance formulas to find the radius of the curve.

Complete step-by-step answer:

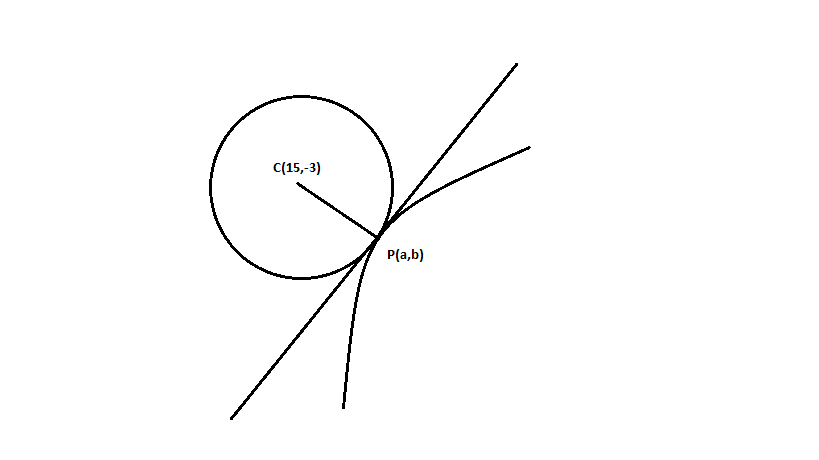
Let Centre of the Circle be C having coordinates $(15, - 3)$. Let the point where the circle touches the tangent to the curve $y = \dfrac{{{x^2}}}{3}$ be $P$ having coordinates $(a,b)$. Since the tangent is touching the circle also we can say that it is a common tangent for the circle as well.
Using the property of Circle, that a line segment from the centre of the circle touching the tangent of the circle is perpendicular to the tangent.
$\therefore $We can Say that CP is Perpendicular to the tangent .
Since the 2 lines that are the tangent and CP are perpendicular to each other we can say that the product of their slopes is $ - 1$.
${m_{CP}} \times {m_{tangent}} = - 1$
In order to find the slope of CP we can use formula $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$as we have coordinates of both the points.
\[\therefore {m_{CP}} = \dfrac{{b + 3}}{{a - 15}}.............(1)\]
Slope of the tangent is the same as the slope of the curve. In order to find the slope of the curve we will differentiate the equation $y = \dfrac{{{x^2}}}{3}$.
$\therefore {m_{tangent}} = \dfrac{d}{{dx}}(\dfrac{{{x^2}}}{3})$
$\therefore {m_{tangent}} = (\dfrac{{2x}}{3})..............(2)$
Since the tangent touches the curve at $P(a,b)$,we will substitute the value of $x = a$ in Equation $1$.
$\therefore {m_{tangent}} = \dfrac{{2a}}{3}..........(3)$
Thus from equation $1\& 3$ we can write the following step
$\therefore \dfrac{{2a}}{3} \times \dfrac{{b + 3}}{{a - 15}} = - 1..........(4)$
Solving further we get the equation as follows
$2a(b + 3) = - 3(a - 15)..........(5)$
We also know that Point P lies on the curve. So, the coordinates of the Point P satisfy the equation of the curve. Thus we can say that
$b = \dfrac{{{a^2}}}{3}..........(6)$
Thus substituting value of $b$ from equation $6$ in equation $5$, we get following equation
$2a(\dfrac{{{a^2}}}{3} + 3) = - 3(a - 15)..........(7)$
Simplify the equation we get
\[\dfrac{{2{a^3}}}{3} + 6a = - 3a + 45..........(8)\]
Taking LCM and removing the denominator
\[2{a^3} + 27a - 135 = 0..........(9)\]
Now , to find the solution we will have to look for a positive value of $a$ which satisfies the solution as it lies in the first quadrant. On trial and error we see that $a = 3$ satisfies the equation $9$.
Value of $b$ from equation $6$ we get as $\dfrac{{{3^2}}}{3}i.e.3$
Coordinates of Point P are $(3,3)$.
Since we have coordinates of both the points C & P, we can now find the Radius of the circle. From the figure we can say that CP is the radius of the circle. Thus the distance of Line CP is the radius of the circle. We will have to use the distance formula to find Radius of the circle.
$CP = \sqrt {{{(15 - 3)}^2} + {{( - 3 - 3)}^2}} $
Radius of the circle is $\sqrt {{{12}^2} + {6^2}} $ =$\sqrt {180} $
We can write $\sqrt {180} $ as $\sqrt {36 \times 5} $.
$\therefore $Radius = $6\sqrt 5 $.

Answer is Option $D - 6\sqrt 5 $

Note: While solving sums from the chapter curves, Student has to first draw the curve and all represent all the data through graphical representation. Once the representation is done it becomes easy to decide which approach to follow. While solving such a type of numerical student should have thorough knowledge about the properties of the curves.