Question

A circle with a radius of one inch has an area of about how many square inches?

Answer 1

Hint: In the above problem, we have given a circle with a radius measurement as 1 inch and we are asked to find the area of the circle. We know that area of the circle is equal to $\pi {{r}^{2}}$. So, to find the area of the above figure, we have to put the “r” value as 1 inch in this formula for the area of the circle.

Complete step by step solution:
In the figure, given above, radius if the circle is given as 1 inch so marking this radius of 1 inch in the above figure we get,

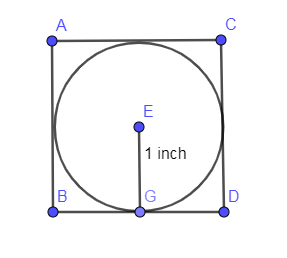
Now, we are asked to find the area of this circle having radius as 1 inch. In the above figure, you can see that EG is the radius of the given circle and has a radius value as 1 inch.
We know that the area of the circle is equal to:
$\pi {{r}^{2}}$
So, substituting the value of “r” as 1 inch in the above formula we get,
$\pi {{\left( 1inch \right)}^{2}}$
We also know that the value of $\pi =3.14$ so substituting the value of $\pi =3.14$ in the above expression we get,
$\begin{align}
  & =\left( 3.14 \right){{\left( 1inch \right)}^{2}} \\
 & =3.14{{\left( inch \right)}^{2}} \\
\end{align}$
In the above expression, we can write ${{\left( inch \right)}^{2}}=\text{sq}\text{. inches}$
As you can see that our answer is in the square inches which is the requirement of the problem so we have found out the area as 3.14 square inches.

Note: In the above solution, instead of putting the value of $\pi =3.14$, you can also put the value of $\pi =\dfrac{22}{7}$. Then after substituting the value of $\pi =\dfrac{22}{7}$ in the above area of circle formula we get,
$\begin{align}
  & \dfrac{22}{7}{{\left( 1inch \right)}^{2}} \\
 & =\dfrac{22}{7}{{\left( inch \right)}^{2}} \\
\end{align}$