Question

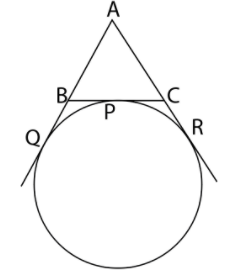
A circle touches the side BC of $\Delta ABC$ at P and touches AB and AC produced at Q and R respectively. Prove that $AQ = \dfrac{1}{2}\left( {Perimeter\,\,of\,\,\Delta ABC} \right)$

Answer 1

Hint:
Firstly, draw a neat diagram of the information provided in the question.
Then, use the property that the tangents to a circle from any given point lying out of the circle are equal in length.
Also, the perimeter of the triangle ABC can be given by the sum of the lengths of sides of the triangle.
Thus, solve the perimeter by using appropriate notations.

Complete step by step solution:
Here, we will firstly draw a neat diagram of the information given in the question.

We know that the tangents to a circle from any given point lying out of the circle are equal in length.
Also, we can see that AQ and AR are the tangents drawn from the point A to the circle, BP and BQ the tangents drawn from the point B to the circle and CP and CR the tangents drawn from the point C to the circle.
So, AQ = AR ... (1)
BP = BQ ... (2)
CR = CP ... (3)
Now, the perimeter of the triangle ABC can be given by the sum of the lengths of sides of the triangle.
Thus, Perimeter of triangle \[ABC = AB + BC + AC\]
From the diagram, we can see that \[BC = BP + PC\]and\[AC = AR-CR\].
So, Perimeter of triangle \[ABC = AB + BP + PC + AR-CR\]
But, from equations (2) and (3), we substitute BP by BQ, AR by AQ and CR by CP or PC.
So, Perimeter of triangle \[ABC = AB + BQ + PC + AQ-PC\]
Also, from figure, we can say that \[AB + BQ\] is equal to AQ
Therefore, Perimeter of triangle \[ABC = AQ + AQ = 2AQ\]
Now, half of the perimeter of the triangle \[ = \dfrac{1}{2} \times AQ\] = AQ.

Thus, we proved, $AQ = \dfrac{1}{2}\left( {Perimeter\,\,of\,\Delta ABC} \right)$.

Note:
The circle drawn here in the figure is also known as an excircle.
Excircle:
A circle in which the centre of the circle is the point of intersection of angle bisector of opposite angle and the exterior angle bisectors of the other two angles of the triangle is called an excircle.