Question

A circle through the points $A\left( 1,0 \right)$ and $B\left( 5,0 \right)$ touches the $y$axis at $C\left( 0,\lambda \right).$ If $\angle ACB$ is maximum, then
(a) $\left| \lambda \right|=\sqrt{5}$
(b) $\left| \lambda \right|=\sqrt[2]{5}$
(c) $\left| \lambda \right|=\sqrt[3]{5}$
(d) $\left| \lambda \right|=\sqrt[4]{5}$

Answer 1

Hint: Assume an arbitrary equation of a circle and find out the parameters by satisfying the equation with the coordinates of the points which the circle passes through, as given in the question. First let’s see what the diagram of the circle would look like by drawing it on the coordinate system with the specifics mentioned in the question. Thus, the circle would look like this on a graph :

Complete step-by-step answer:

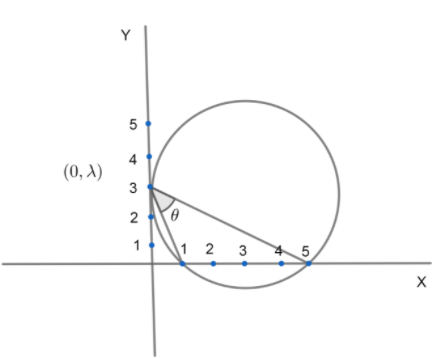
We will now take the arbitrary equation of the circle as :
\[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\], where its centre is$\left( a,b \right)$and $r$ is the radius of the circle.
Now, we can clearly see that the circle passes through the point $A(1,0)$. So, from point $A\left( 1,0 \right)$ , we can satisfy the arbitrary equation we assumed, and doing so, we get
$\begin{align}
  & {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}};x=1,y=0 \\
 & \to {{(1-a)}^{2}}+{{(0-b)}^{2}}={{r}^{2}} \\
\end{align}$
$\to {{\left( 1-a \right)}^{2}}+{{b}^{2}}={{r}^{2}}$
\[\to {{\left( 1-a \right)}^{2}}={{r}^{2}}-{{b}^{2}}.....................(1)\]
Similarly, we also know that the circle passes through the point $B(5,0)$. So, we can make it satisfy the arbitrary equation too. Doing so, from point $B\left( 5,0 \right)$ , we get :
$\begin{align}
  & {{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}};x=5,y=0 \\
 & \to {{(5-a)}^{2}}+{{(0-b)}^{2}}={{r}^{2}} \\
\end{align}$
\[\begin{align}
  & \to {{\left( 5-a \right)}^{2}}+{{b}^{2}}={{r}^{2}} \\
 & \to {{\left( 5-a \right)}^{2}}={{r}^{2}}-{{b}^{2}}....................(2) \\
\end{align}\]
From equation $(1)$ and equation $(2)$, we get that,
$\begin{align}
  & {{\left( 1-a \right)}^{2}}=({{r}^{2}}-{{b}^{2}})={{\left( 5-a \right)}^{2}} \\
 & \to {{(1-a)}^{2}}={{(5-a)}^{2}} \\
\end{align}$
Now, let’s take the square root of both sides, but remember, while taking the square root of the squares we have, we can get the result as both, a positive, as well as a negative square root. So, be sure to consider both the cases.
Thus, taking square roots of both the sides, we get :
$\begin{align}
  & \to \pm (1-a)=\pm (5-a) \\
 & \to (1-a)=\pm (5-a) \\
 & \to 1-a=5-a;1-a=-5+a \\
 & \to 1=5;2a=6 \\
 & \to (impossible);a=3 \\
\end{align}$
Hence, since the answer we got from taking the positive result of the square root would never be correct ( since $1\ne 5$), we choose the answer we got from taking the negative square root.
Hence, $a=3$.
Now, let’s substitute the value of $a$ we found out, in the arbitrary equation that we had assumed.
So, putting $a=3$ in that, we get new circle equation as :
\[{{\left( x-3 \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\]
Now, we have that $\angle ACB$ is maximum then circle touches y axis at $\left( 0,\lambda \right)$, so we can conclude that the $y$ axis, or the line $(x=0)$ acts as a tangent at $C$.
Thus, $\left( x=0 \right)$ , is a tangent at $\left( 0,\lambda \right)$ point.
On differentiating the arbitrary equation in terms of $x$, to find the slope of the tangent at any point on the circle, we’ll get :
$\dfrac{d{{(x-3)}^{2}}}{dx}+\dfrac{d{{(y-b)}^{2}}}{dx}=\dfrac{d{{r}^{2}}}{dx}$
\[\left( x-3 \right)+\left( y-b \right)\dfrac{dy}{dx}=0\]
\[\dfrac{dy}{dx}=\dfrac{-\left( x-3 \right)}{\left( y-b \right)}=\dfrac{3-x}{y-b}\]
Therefore, to find out the tangent’s slope at the point $C(0,\lambda )$, we’ll substitute $x=0,y=\lambda $ in the equation for the slope of the tangent, or in the equation of $\dfrac{dy}{dx}$.
Thus, $\dfrac{dy}{dx}$ at point $C={{\left. \dfrac{dy}{dx} \right|}_{\left( 0,\lambda \right)}}=\dfrac{3-0}{\lambda -b}=\dfrac{3}{\lambda -b}$
Since, the slope of the $y$axis is $\infty $(infinity), the slope of our tangent should also be infinite.
The slope becomes infinity only when the denominator is $0$.
i.e.$\begin{align}
  & \therefore \left( \lambda -b \right)=0 \\
 & \therefore \\
\end{align}$
Now, we’ll have a new circle equation, by putting$\left( \lambda =b \right)$. Doing so, we get :
\[\to {{\left( x-3 \right)}^{2}}+{{\left( y-\lambda \right)}^{2}}={{r}^{2}}\]
Now, putting point $C\left( 0,\lambda \right)$in the new equation, it becomes :
$\to {{\left( 0-3 \right)}^{2}}+{{\left( \lambda -\lambda \right)}^{2}}={{r}^{2}}$
$\begin{align}
  & \to 9+0={{r}^{2}} \\
 & \to \\
\end{align}$
Hence, radius comes out to be $3$ units.
Now, circle equation becomes :
$\to {{\left( x-3 \right)}^{2}}+{{\left( y-\lambda \right)}^{2}}={{3}^{2}}...................(3)$
Now, put $\left( 1,0 \right)$ in equation $(3)$. Doing so, we get :
$\begin{align}
  & {{\left( 1-3 \right)}^{2}}+{{\left( y-\lambda \right)}^{2}}={{3}^{2}} \\
 & 4+{{\lambda }^{2}}=9 \\
 & {{\lambda }^{2}}=5 \\
 & \therefore \\
\end{align}$
But, the value asked to us is of $|\lambda |=|\pm \sqrt{5}|=\sqrt{5}$
Therefore, $|\lambda |=\sqrt{5}$
Therefore, the correct answer is option (a).

Note: Most mistakes made by students are in solving the equation of circle i.e.${{\left( {{x}_{1}}-h \right)}^{2}}+{{\left( {{y}_{1}}-k \right)}^{2}}={{r}^{2}}$ and then finding out the value of $'\lambda '$. Finding the value of $'\lambda '$ depends on the condition given in the question. Here it is given to be with respect to $\angle ACB$, i.e. $\lambda $ should be such that $\angle ACB$ is maximum. So, we can use the concept that when $\angle ACB$ is maximum then the circle touches y axis at $\left( 0,\lambda \right)$. Hence, be careful when putting a point’s coordinates in the equation of the circle and do calculations correctly.