Question

A circle of radius ‘a’ is divided into 6 equal sectors. An equilateral triangle is drawn on the chord of each sector to lie outside the circle. Area of the resulting figure is:

Answer 1

Hint: We will find the area of the triangle inside the circle and then find the area of the triangle outside the circle. We will add both the obtained area to get the resulting area of the figure. Please note that area of an equilateral triangle = $\dfrac{\sqrt{3}{{a}^{2}}}{4}$.

Complete step by step answer:
It is given in the question that a circle of radius ‘a’ is divided into 6 equal sectors. An equilateral triangle is drawn on the chord of each sector to lie outside the circle, then we have to find out the area of the resulting figure.

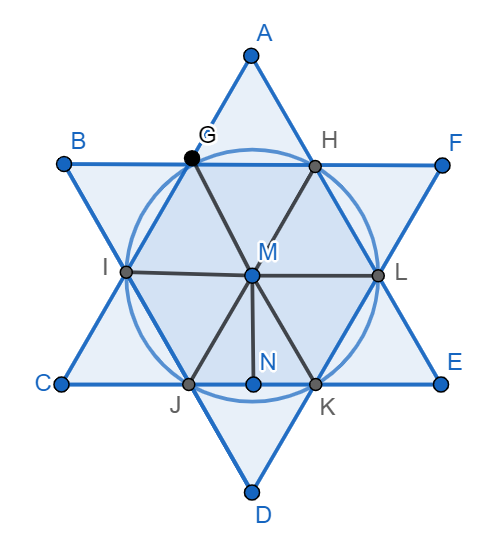
It is clear from the figure that all the angles subtended at the centre of the circle have equal measurement, because all the triangles are made by the same radii of the circle which is ‘a’ and they also have the same equal sector.
So $\Delta MGH=\Delta MHL=\Delta MKL=\Delta MKJ=\Delta MJI=\Delta MIG$, all these 6 triangles are isosceles triangles.
We will consider $\Delta MJK$ for our calculation and then multiply it with 6 so that we will get the area of all 6 triangles inside the circle together.
We will construct a perpendicular MN from M to JK, we will get two triangles $\Delta MNK$ and $\Delta MNJ$. We know that JK is a chord of a circle which is equal to 60 degrees. So, $\angle JMK={{60}^{{}^\circ }}$. So, from this we can say that $\angle NMK={{30}^{{}^\circ }}$ because it is half of $\angle JMK$.
Now, \[length\text{ }of\text{ }chord\text{ }JK\text{ }=2\times radius\times \sin \left( \dfrac{\angle JMK}{2} \right)\]. Here, \[radius\text{ }=\text{ }6cm\] and $\angle JMK={{60}^{{}^\circ }}$. Therefore, \[we\text{ }get\text{ }length\text{ }of\text{ }chord\text{ }=2\times 6\times \dfrac{1}{2}=6cm\].
We know that NK is half of JK, so. $NK=3cm$.
Now, we know that JNK is a right angled triangle and according to pythagoras theorem the sum of base square and height square is equal to hypotenuse square. So,
${{h}^{2}}+{{3}^{3}}={{6}^{3}}$, solving further,
${{h}^{2}}=36-9=25$
$h=\pm 5cm$.
Since length cannot be negative therefore $h=5cm$. We know that \[area\text{ }of\text{ }triangle\text{ }=\dfrac{1}{2}\times base\times height\]. We have $base=5cm,height=5cm$. So, the area of$\Delta MJK=\dfrac{1}{2}\times JK\times h$ = $\dfrac{1}{2}\times 6\times 5=15sq.unit$.
It is noted that all the triangles $\Delta MGH,\Delta MHL,\Delta MKL,\Delta MKJ,\Delta MJI,\Delta MIG$ have the same area which is 15 sq. Unit.
Now, the triangle outside the circle JKD is an equilateral triangle, its side length is equal to the chord to the circle, and the chord of the circle is 6cm. We know that area of the equilateral triangle is $\dfrac{\sqrt{3}{{a}^{2}}}{4}$. Here $a=6$, so area of $\Delta JKD$ = $\dfrac{\sqrt{3}\times {{\left( 6 \right)}^{2}}}{4}=\dfrac{\sqrt{3}\times 36}{4}=9\sqrt{3}$ sq.unit.
Now, the resulting figure area is given by \[all\text{ }the\text{ }inner\text{ }triangles\text{ }area\text{ }+\text{ }all\text{ }outer\text{ }triangle\text{ }area\] = $6\times 15+6\left( 9\sqrt{3} \right)=90+90.52=183.52sq.unit$.
Therefore, the resulting area of the figure will be 183.52 sq.units.

Note: Students may directly calculate the area of figure by finding the area of the outsider triangle and the area of the circle, they may add these two areas and declare their answer. But this is incorrect. If we add an area of the circle with an outsider area then some extra area will be added and result in formation of wrong answers.