Question

A circle of largest area is cut from a rectangular piece of cardboard with dimensions 55cm and 42cm. Find the ratio between the area of the circle cut and the area of the remaining cardboard.
\[\begin{align}
  & A.3:2 \\
 & B.5:2 \\
 & C.7:2 \\
 & D.7:8 \\
\end{align}\]

Answer 1

Hint: In this question, we are given that, the largest circle is cut from a rectangular piece of cardboard with given dimensions. We need to find the ratio between the area of the circle cut and the area of the remaining cardboard. For this, we will first find the diameter of the circle which will produce the largest circle. Then we will find the area of the circle and the area of the cardboard. Subtracting both areas will give us the area of the remaining cardboard. At last using areas found we will find our required ratio.

Complete step by step answer:
Here we need to find the area of the circle the largest circle that can be cut from rectangular cardboard. The dimensions of the cardboard are 55cm and 42cm. For largest circle, the diameter of the circle has to be either 55cm or 42cm. If we take the diameter as 55cm, the circle will come out of the cardboard because of the smaller width. Hence, the diameter of the circle will be 42cm. Our diagram looks like this,

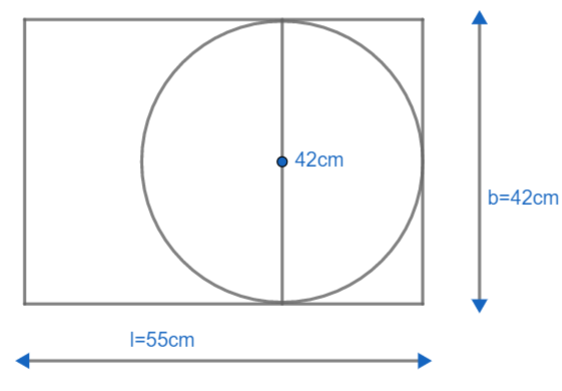
Now we need to find the area of the circle and the area of the remaining cardboard.
We know that, the radius of a circle is half of the diameter of a circle.
Therefore, radius of circle = $ \dfrac{1}{2} $ diameter of circle.
 $ \Rightarrow \dfrac{1}{2}\times 42=21cm $ .
Therefore, r = 21cm.
Now we know that the area of a circle with radius r is given by $ \pi {{r}^{2}} $.
So area of circle with radius r = 21cm will be equal to,
\[\begin{align}
  & \text{Area}=\pi \times {{\left( 21 \right)}^{2}} \\
 & \Rightarrow 21\times 21\times \pi c{{m}^{2}} \\
 & \Rightarrow 21\times 21\times \dfrac{22}{7}c{{m}^{2}} \\
 & \Rightarrow 3\times 21\times 22c{{m}^{2}} \\
 & \Rightarrow 1386c{{m}^{2}} \\
\end{align}\]
Hence the area of the circle is $ 1386c{{m}^{2}} $ .
For finding the area of the remaining cardboard, we need to subtract the area of the circle from the area of the cardboard. So let's find the area of the cardboard.
Length of the cardboard = 55cm.
Breadth of the cardboard = 42cm.
Area of a rectangle is given by $ \text{length}\times \text{breadth} $ .
There, area of the rectangular cardboard \[\Rightarrow \left( 55\times 42 \right)c{{m}^{2}}=2310c{{m}^{2}}\].
Area of the remaining cardboard = area of the cardboard - area of the circle.
Area of the remaining cardboard $ \Rightarrow \left( 2310-1386 \right)c{{m}^{2}}=924c{{m}^{2}} $ .
Now for finding the ratio of the area of the circle to the area of the remaining cardboard. Let us write in division form, we get,
 $ \dfrac{\text{Area of circle}}{\text{Area of remaining cardboard}}=\dfrac{1386c{{m}^{2}}}{924c{{m}^{2}}} $ .
Simplifying it and dividing the numerator and denominator by 6, we get $ \dfrac{231}{154} $ .
Dividing the numerator and the denominator by 7 we get $ \dfrac{33}{22} $ .
Dividing the numerator and the denominator by 11, we get $ \dfrac{3}{2} $ .
In ratio form,
Area of circle: area of remaining cardboard = 3:2.
Hence option A is the correct answer.
Note:
 Take care of the units while finding the ratio. Make sure units of both quantities are the same. Keep in mind the formula of the areas of the various figures. Take care of calculation while finding ratio. Do not forget to write the units after finding any measurements.